题目内容
空间四边形ABCD中,平行于对角线AC、BD的平面分别交AB、BC、CD、DA于点E、F、G、H,且AC⊥BD,AC=a,BD=b,求四边形EFGH面积的最大值.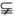
思路分析:判断四边形EFGH是矩形,利用矩形的面积公式建立目标函数,求最值.
解:由BD∥平面EFGH,且BD![]() 平面ABD,平面ABD∩平面EFGH=EH,知EH∥BD,同理,FG∥BD.
平面ABD,平面ABD∩平面EFGH=EH,知EH∥BD,同理,FG∥BD.
故EH∥FG.同理,EF∥HG.
故四边形EFGH是平行四边形.
由BD⊥AC,知EF⊥EH,从而∠HEF=90°.故平行四边形EFGH是矩形.
设EF=x,由相似三角形知![]() ,∴
,∴![]() .
.
∴![]() ,得FG=
,得FG=![]() .
.
∴S四边形EFGH=FG·EF
=![]() x=
x=![]() (ax-x2)
(ax-x2)
=![]() [-(x-
[-(x-![]() )2+
)2+![]() ].
].
当x=![]() 时,四边形EFGH面积最大,最大值为
时,四边形EFGH面积最大,最大值为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点.
如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点. 如图,空间四边形ABCD中,AB、BC、CD的中点分别是P、Q、R,且
如图,空间四边形ABCD中,AB、BC、CD的中点分别是P、Q、R,且