题目内容
如图，平行四边形ABCD中，AE：EB=1：2，若△AEF的面积为6，则△ABC的面积为（ ）分析：由已知中平行四边形ABCD中，AE：EB=1：2，若△AEF的面积为6，利用相似三角形性质，可得S△CDF的大小，根据等高三角形，底边之比等于面积之比，可得S△ADF的值，进而得到△ABC的面积
解答：解：∵ABCD为平行四边形
∴AB平行于CD
∴△AEF∽△CDF
∵AE：EB=1：2
∴AE：CD=AE：AB=1：3
∴S△CDF=32×S△AEF=9×6=54
∵AF：CF=AE：CD=1：3
∴S△ADF=S△CDF÷3=54÷3=18
∴S△ABC=S△ACD=S△CDF+S△ADF=54+18=72
故选D
∴AB平行于CD
∴△AEF∽△CDF
∵AE：EB=1：2
∴AE：CD=AE：AB=1：3
∴S△CDF=32×S△AEF=9×6=54
∵AF：CF=AE：CD=1：3
∴S△ADF=S△CDF÷3=54÷3=18
∴S△ABC=S△ACD=S△CDF+S△ADF=54+18=72
故选D
点评：本题考查的知识点是相似三角形的判定与性质，其中熟练掌握相似三角形面积之比等于相似比平方的性质，是解答本题的关键．
练习册系列答案
星级口算天天练系列答案
相关题目
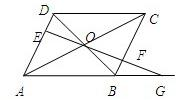如图，平行四边形ABCD的对角线交于点O，过点O的直线交AD于E，BC于F，交AB延长线于G，已知AB=a，BC=b，BG=c，则BF=
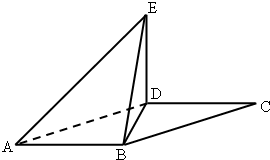如图，平行四边形ABCD中，∠DAB=60°，AB=2，AD=4将△CBD沿BD折起到△EBD的位置，使平面EDB⊥平面ABD．
如图，平行四边形ABCD中，E，F分别是BC，DC的中点，G为交点，若
（2012•枣庄一模）如图，平行四边形ABCD中，点E是边BC（靠近点B）的三等分点，F是AB（靠近点A）的三等分点，P是AE与DF的交点，则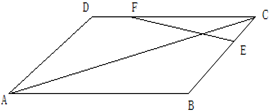
如图，平行四边形ABCD中，