题目内容
已知函数
（Ⅰ）当
时, 求函数
的单调增区间；
（Ⅱ）求函数在区间
上的最小值；
（Ⅲ） 在（Ⅰ）的条件下，设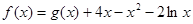
,
证明：
.参考数据：
．
（Ⅰ）当
时, 求函数的单调增区间；（Ⅱ）求函数
在区间上的最小值；（Ⅲ） 在（Ⅰ）的条件下，设
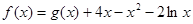,证明：
.参考数据：．（Ⅰ）
（Ⅱ）
（Ⅲ）用放缩法证明.
（Ⅱ）（Ⅲ）用放缩法证明.
试题分析：(Ⅰ)当
时，
，
或
。函数
的单调增区间为 (Ⅱ)
，
当
，
单调增。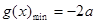
当
，
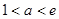单调减. 
单调增。
当
，
单调减，
（Ⅲ）令
，
, 
即
,
，
点评：本题考查函数的单调区间和函数的最小值的求法，而利用单调性证明不等式是难题．解题时要认真审题，仔细解答．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
在点(0,f(0))处的切线方程；
∈[1，1]，使得
（e是自然对数的底数），求实数
的取值范围.
. 
时取得极值？说明理由；
,4］时，函数f(x)与g(x)的图像有两个公共点，求c的取值范围. 
，解不等式
；
的不等式
． 
； 
，求证：
≤
.
分）
在定义域
内某区间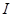
上是增函数，而
在
在
，
在
是否是“弱增函数”，
(
是常数且
)在
上是“弱增函数”．
是以
为周期的偶函数，当
时，
．若关于
的方程
（
）在区间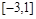
内有四个不同的实根，则
的取值范围是
