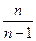题目内容
(本小题满分14分)已知函数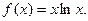 (Ⅰ)求函数
(Ⅰ)求函数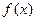 的单调区间和最小值;
的单调区间和最小值;
(Ⅱ)当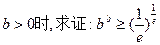 (其中e="2.718" 28…是自然对数的底数);
(其中e="2.718" 28…是自然对数的底数);
(Ⅲ)若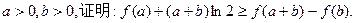
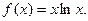 (Ⅰ)求函数
(Ⅰ)求函数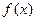 的单调区间和最小值;
的单调区间和最小值;(Ⅱ)当
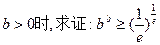 (其中e="2.718" 28…是自然对数的底数);
(其中e="2.718" 28…是自然对数的底数);(Ⅲ)若
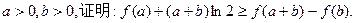
(Ⅰ) (Ⅱ)略 (Ⅲ)略
(Ⅱ)略 (Ⅲ)略
 (Ⅱ)略 (Ⅲ)略
(Ⅱ)略 (Ⅲ)略(Ⅰ) …………1分
…………1分
 上是单调递增函数.
上是单调递增函数.
 同理,令
同理,令
∴f(x)单调递增区间为 ,单调递减区间为
,单调递减区间为 .……2分
.……2分
由此可知 ……1分
……1分
(Ⅱ)由(I)可知当 时,有
时,有 ,
,
即 .
.  .……………3分
.……………3分
(Ⅲ)将 变形,得
变形,得
 ,
,
即证明
设函数 …………3分
…………3分

∴函数 )上单调递增,在
)上单调递增,在 上单调递减.
上单调递减.
∴ 的最小值为
的最小值为 ,即总有
,即总有
而
 即
即 令
令
则

 …分
…分
 …………1分
…………1分 上是单调递增函数.
上是单调递增函数. 同理,令
同理,令
∴f(x)单调递增区间为
 ,单调递减区间为
,单调递减区间为 .……2分
.……2分由此可知
 ……1分
……1分(Ⅱ)由(I)可知当
 时,有
时,有 ,
,即
 .
.  .……………3分
.……………3分(Ⅲ)将
 变形,得
变形,得 ,
,即证明

设函数
 …………3分
…………3分
∴函数
 )上单调递增,在
)上单调递增,在 上单调递减.
上单调递减.∴
 的最小值为
的最小值为 ,即总有
,即总有
而

 即
即 令
令
则


 …分
…分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
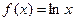 ,
, ,函数
,函数 的图象与x轴的交点也在函数
的图象与x轴的交点也在函数 的图象上,且在此点有公切线. (1)求
的图象上,且在此点有公切线. (1)求 、
、 的值;(2)对任意
的值;(2)对任意 的大小.
的大小. , 过点Q
, 过点Q 作C的切线
作C的切线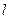 , 切点为P.
, 切点为P.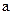 怎样变化, 点P总在一条定直线上;
怎样变化, 点P总在一条定直线上;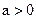 , 过点P且与
, 过点P且与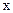 轴交于点T, 求
轴交于点T, 求 的最小值(O为原点).
的最小值(O为原点).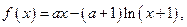 其中
其中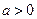 。(1)求
。(1)求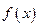 的单调区间;
的单调区间;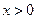 时,证明不等式:
时,证明不等式: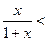
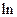
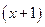
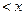 ;
;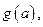 证明不等式:
证明不等式: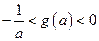 。
。 在
在 上单调递减,在(1,3)上单调递增在
上单调递减,在(1,3)上单调递增在 上单调递减,且函数图象在
上单调递减,且函数图象在 处的切线与直线
处的切线与直线 垂直.
垂直. 、
、 、
、 的值;(Ⅱ)设函数
的值;(Ⅱ)设函数 =0有三个不相等的实数根,求
=0有三个不相等的实数根,求 的取值范围.
的取值范围.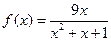 (
(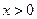 ) , (Ⅰ)试确定
) , (Ⅰ)试确定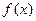 的单调区间 , 并证明你的结论 ;(Ⅱ)若
的单调区间 , 并证明你的结论 ;(Ⅱ)若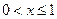 时 , 不等式
时 , 不等式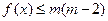 恒成立 , 求实数
恒成立 , 求实数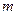 的取值范围 .
的取值范围 . 
 的导函数
的导函数 ,则数列
,则数列 的前n项和是
的前n项和是