题目内容
已知:集合 ,集合B={y|y=x2-2x+3,x∈[0,3]},求A∩B.
,集合B={y|y=x2-2x+3,x∈[0,3]},求A∩B.
解:由集合A中的函数y=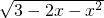 ,得到3-2x-x2≥0,
,得到3-2x-x2≥0,
分解因式得:(x+3)(x-1)≤0,
解得:-3≤x≤1,
∴A={x|-3≤x≤1},
由集合B中函数y=x2-2x+3=(x-1)2+2,x∈[0,3],得到2≤y≤6,
∴B={y|2≤y≤6},
则A∩B=∅.
分析:根据负数没有平方根求出集合A中函数的定义域,确定出集合A,根据二次函数的性质,求出集合B中函数的值域,确定出集合B,找出A与B的公共部分,即可确定出两集合的交集.
点评:此题属于以函数的定义域与值域为平台,考查了交集及其运算,熟练掌握交集的定义是解本题的关键.
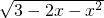 ,得到3-2x-x2≥0,
,得到3-2x-x2≥0,分解因式得:(x+3)(x-1)≤0,
解得:-3≤x≤1,
∴A={x|-3≤x≤1},
由集合B中函数y=x2-2x+3=(x-1)2+2,x∈[0,3],得到2≤y≤6,
∴B={y|2≤y≤6},
则A∩B=∅.
分析:根据负数没有平方根求出集合A中函数的定义域,确定出集合A,根据二次函数的性质,求出集合B中函数的值域,确定出集合B,找出A与B的公共部分,即可确定出两集合的交集.
点评:此题属于以函数的定义域与值域为平台,考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
 ,集合B={y|y=2x}.
,集合B={y|y=2x}.