题目内容

设f(x)=ax+(a＞0)，

(1)判断函数f(x)在(0,+∞)上的单调性.

(2)设f(x)在0＜x≤1上最小值为g(a),求y=g(a)的解析式.

解：(1)∵f(x)=ax+-,

∴f′(x)=a-==.

∵a＞0,x＞0.∴f′(x)=0.得x=.

∴当0＜x＜时，f′(x)＜0.

∴f(x)在(0,)上是减函数.

当x＞时f′(x)＞0,

∴f(x)在［,+∞上是单调增函数.

(2)∵0＜x≤1，∴当≤1即a≥1时，g(a)=f()=1+1-=2-.

当＞1即0＜a＜1时，g(a)=f(1)=a,

∴g(a)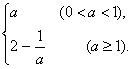


练习册系列答案
相关题目
设f(x)=
a
x
+xlnx，g（x）=x3-x2-3．
（1）当a=2时，求曲线y=f（x）在x=1处的切线方程；
（2）如果存在x1，x2∈[0，2]，使得g（x1）-g（x2）≥M成立，求满足上述条件的最大整数M；
（3）如果对任意的s，t∈[
1
2
，2]，都有f（s）≥g（t）成立，求实数a的取值范围．
设f(x)=
ax+a-x
2
，g(x)=
ax-a-x
2
（其中a＞0，且a≠1）．
（1）5=2+3请你推测g（5）能否用f（2），f（3），g（2），g（3）来表示；
（2）如果（1）中获得了一个结论，请你推测能否将其推广．
设f(x)=a
x
-lnx（a＞0）：
（1）若f（x）在[1，+∞）上递增，求a的取值范围；  
（2）求f（x）在[1，4]上的最小值．
设f(x)=a
x
-lnx（a＞0）
（1）若f（x）在[1，+∞）上递增，求a的取值范围；
（2）若f（x）在[2，4]上的存在单调递减区间，求a的取值范围．
若函数y=f（x），x∈D同时满足下列条件：
（1）在D内的单调函数；
（2）存在实数m，n，当定义域为[m，n]时，值域为[m，n]．则称此函数为D内可等射函数，设f(x)=
ax+a-3lna
（a＞0且a≠1），则当f （x）为可等射函数时，a的取值范围是
（0，1）∪（1，2）
（0，1）∪（1，2）
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网