题目内容
已知 若
若 的定义域和值域都是
的定义域和值域都是 ,则
,则 .
.
 若
若 的定义域和值域都是
的定义域和值域都是 ,则
,则 .
.5
试题分析:该二次函数开口向上,对称轴为
 ,最小值为
,最小值为 ,所以可分3种情况:
,所以可分3种情况:(1)当对称轴
 在区间
在区间 的左侧时,函数在区间
的左侧时,函数在区间 上单调递增,所以此时
上单调递增,所以此时 ;
;(2) 当对称轴
 在区间
在区间 的右侧时,函数在区间
的右侧时,函数在区间 上单调递减,所以此时
上单调递减,所以此时 ;
;(3) 当对称轴
 在区间
在区间 内时,函数在区间
内时,函数在区间 上单调递减,在区间
上单调递减,在区间 上单调递增,所以此时
上单调递增,所以此时 ,函数在区间
,函数在区间 内的最小1值为1,也是值域的最小值
内的最小1值为1,也是值域的最小值 ,所以
,所以 ,同时可知函数值域的最大值一定大于2.通过计算可知
,同时可知函数值域的最大值一定大于2.通过计算可知 ,所以可知函数在
,所以可知函数在 时取得最大值
时取得最大值 ,即
,即 .所以
.所以 .
.通过验证可知,函数
 在区间
在区间 内的值域为
内的值域为 .
.综上可知:
 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 上恒有f(x)
上恒有f(x) -3成立,求实数a 的取值范围.
-3成立,求实数a 的取值范围.
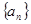 的前n项和为
的前n项和为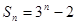 ,则
,则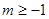 ,则函数
,则函数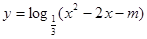 的值域为R;
的值域为R;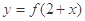 与函数
与函数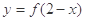 的图象关于直线x=2对称;
的图象关于直线x=2对称;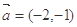 与
与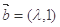 的夹角为钝角,则实数
的夹角为钝角,则实数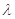 的取值范围是
的取值范围是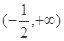 ;
;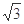 的圆锥,过顶点的一个截面面积的最大值为
的圆锥,过顶点的一个截面面积的最大值为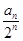 ,求Tn.
,求Tn. 是方程
是方程 的两根,且
的两根,且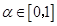 ,
, ,
, ,求
,求 的最大值与最小值之和为( ).
的最大值与最小值之和为( ).