题目内容
已知定义在区间(0,+∞)上的函数f(x)满足f(
)=f(x1)-f(x2),且当x>1时f(x)<0.
(1)求f(1)的值
(2)判断f(x)的单调性
(3)若f(3)=-1,解不等式f(|x|)<2.
| x1 |
| x2 |
(1)求f(1)的值
(2)判断f(x)的单调性
(3)若f(3)=-1,解不等式f(|x|)<2.
(1)令x1=x2得f(1)=0
(2)设x1>x2>0 则
>1,f(
)<0∴f(x1)-f(x2)=f(
)<0
所以f(x)在(0,+∞)为减函数;
(3)∵f(1)=0,f(3)=-1∴f(3)=f(
)=f(1)-f(
)
∴f(
)=f(1)-f(3)=1,f(
)=f(
)-f(3)=2
∴f(|x|)<2?f(|x|)<f(
)?|x|>
所以原不等式的解集为{x|x<-
,或x>
}.
(2)设x1>x2>0 则
| x1 |
| x2 |
| x1 |
| x2 |
| x1 |
| x2 |
所以f(x)在(0,+∞)为减函数;
(3)∵f(1)=0,f(3)=-1∴f(3)=f(
| 1 | ||
|
| 1 |
| 3 |
∴f(
| 1 |
| 3 |
| 1 |
| 9 |
| 1 |
| 3 |
∴f(|x|)<2?f(|x|)<f(
| 1 |
| 9 |
| 1 |
| 9 |
所以原不等式的解集为{x|x<-
| 1 |
| 9 |
| 1 |
| 9 |

练习册系列答案
相关题目

 若
若 的定义域和值域都是
的定义域和值域都是 ,则
,则 .
.
 在区间
在区间 是增函数,则常数a的取值范围是
是增函数,则常数a的取值范围是  ,则
,则 ____
____ 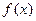 (x∈R)为奇函数,
(x∈R)为奇函数,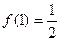 ,
,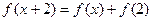 ,则
,则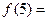 ( )
( ) ;
; 满足
满足
 ,求
,求 ;又若
;又若 ,求
,求 ;
; ,使得
,使得 ,求函数
,求函数