题目内容
已知函数f(x)=x2+ax+1,f(x)在x∈[-3,1 上恒有f(x)
上恒有f(x) -3成立,求实数a 的取值范围.
-3成立,求实数a 的取值范围.
 上恒有f(x)
上恒有f(x) -3成立,求实数a 的取值范围.
-3成立,求实数a 的取值范围.
试题分析:解题思路:
 恒成立,即
恒成立,即 ;利用数形结合讨论对称轴
;利用数形结合讨论对称轴 与区间
与区间 的关系.规律总结:涉及不等式恒成立问题,往往转化为求函数的最值问题;对于一元二次函数求最值,要运用数形结合思想.
的关系.规律总结:涉及不等式恒成立问题,往往转化为求函数的最值问题;对于一元二次函数求最值,要运用数形结合思想.注意点:讨论对称轴
 与区间
与区间 的关系时,要注意运用数形结合思想.
的关系时,要注意运用数形结合思想.试题解析:

(ⅰ)当
 即
即 时,易知
时,易知 在
在 上为增函数,则
上为增函数,则 ,得
,得 ,此时
,此时 无解;
无解;(ⅱ)当
 即
即 时,则
时,则 ,得
,得 ,此时
,此时 ;
;(ⅲ)当
 即
即 时,易知
时,易知 在
在 上为减函数,则
上为减函数,则 ,得
,得 ,此时
,此时 ;
;综上所述,
 的取值范围为
的取值范围为 .
.
练习册系列答案
相关题目
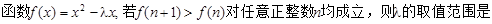 ( )
( ) >0
>0
 若
若 的定义域和值域都是
的定义域和值域都是 ,则
,则 .
.



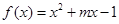 ,若对于任意的
,若对于任意的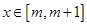 都有
都有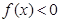 ,则实数
,则实数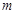 的取值范围为 .
的取值范围为 . 满足
满足
 ,求
,求 ;又若
;又若 ,求
,求 ;
; ,使得
,使得 ,求函数
,求函数