题目内容
设函数f0(x)=|x|,f1(x)=|f0(x)-1|,f2(x)=|f1(x)-2|,则函数f2(x)的图象与x轴所围成图形中的封闭部分的面积是分析:要求函数f2(x)的图象与x轴所围成图形中的封闭部分的面积,先求出函数f2(x)的解析式,由题意可知,根据图象的平移与对称可得到函数f2(x)的图象及解析式,然后利用定积分求出面积即可.
解答:解:根据题意,可由f0(x)的图象向下平移1个单位,然后进行绝对值变换得到f1(x),再把f1(x)向下平移2个单位,再进行绝对值变换得到f2(x)的图象如图所示:
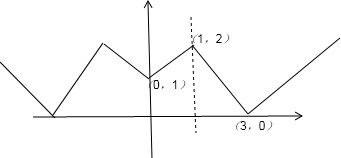
先根据条件分别求出在第一象限,0<x<1时,f2(x)=x+1;当1≤x<3时,f2(x)=-x+3
f2(x)的图象与x轴所围成图形中的封闭部分的面积S=2[∫01(x+1)dx+∫13(-x+3)]=2[(
x2+x|01)+(-
x2+3x|13)]=7
故答案为:7

先根据条件分别求出在第一象限,0<x<1时,f2(x)=x+1;当1≤x<3时,f2(x)=-x+3
f2(x)的图象与x轴所围成图形中的封闭部分的面积S=2[∫01(x+1)dx+∫13(-x+3)]=2[(
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:7
点评:此题是中档题,要求学生会利用平移及绝对值变换得到函数的图象,然后才能利用定积分求面积.学生做题时应当把函数图象画出来,然后数形结合才能得到解题思路.

练习册系列答案
相关题目