题目内容
设函数 ,
, ,
, .
.
(1)若 ,求
,求 的单调递增区间;
的单调递增区间;
(2)若曲线 与
与 轴相切于异于原点的一点,且
轴相切于异于原点的一点,且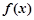 的极小值为
的极小值为 ,求
,求 的值.
的值.
 ,
, ,
,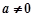 .
. (1)若
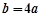 ,求
,求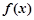 的单调递增区间;
的单调递增区间;(2)若曲线
 与
与 轴相切于异于原点的一点,且
轴相切于异于原点的一点,且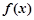 的极小值为
的极小值为 ,求
,求 的值.
的值. (1)证明过程详见解析(2) 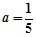 ,
,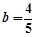 .
.
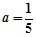 ,
,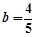 .
.试题分析:
(1)将条件
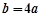 带入函数解析式消b,得到
带入函数解析式消b,得到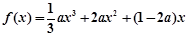 ,对该三次函数求导得到导函数,由于
,对该三次函数求导得到导函数,由于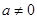 ,故该导函数为二次函数,根据题意需要求的该二次函数大于0的解集,因为二次函数含参数,故依次讨论开口,
,故该导函数为二次函数,根据题意需要求的该二次函数大于0的解集,因为二次函数含参数,故依次讨论开口, 的符号和根的大小,即可到导函数大于0的解集即为原函数的单调增区间.
的符号和根的大小,即可到导函数大于0的解集即为原函数的单调增区间.(2)分析题意,可得该三次函数过原点,根据函数
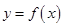 与x轴相切,所以有个极值为0且有一个重根,故可得函数
与x轴相切,所以有个极值为0且有一个重根,故可得函数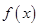 有一个极大值0和一个极小值
有一个极大值0和一个极小值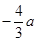 ,有一个重根,则对
,有一个重根,则对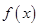 因式分解会得到完全平方式,即
因式分解会得到完全平方式,即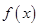 提取x的公因式后,剩下二次式的判别
提取x的公因式后,剩下二次式的判别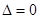 ,得到a,b之间的关系式,再根据极小值为
,得到a,b之间的关系式,再根据极小值为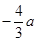 ,则求导求出极小值点,得到关于a,b的另外一个等式,即可求出a,b的值.
,则求导求出极小值点,得到关于a,b的另外一个等式,即可求出a,b的值.试题解析:
(1)
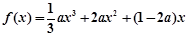 ,
,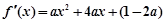 .
.令
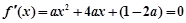 ,
,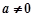 ,
,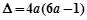
当
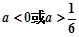 时,由
时,由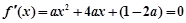 得
得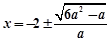 .
.①当
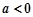 时,
时,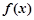 的单调递增区间为
的单调递增区间为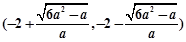 ; 3分
; 3分②当
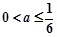 时,
时,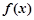 的单调递增区间为
的单调递增区间为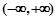 ; 5分
; 5分③当
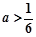 时,
时,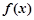 的单调递增区间为
的单调递增区间为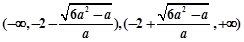 . 7分
. 7分(2)
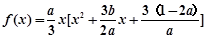 ,
, 依据题意得:
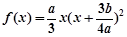 ,且
,且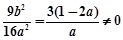 ① 9分
① 9分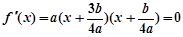 ,得
,得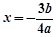 或
或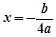 . 11分
. 11分因为
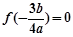 ,所以极小值为
,所以极小值为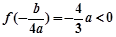 ,
,∴
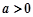 且
且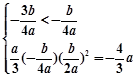 ,得
,得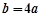 , 13分
, 13分代入①式得
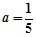 ,
,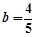 . 15分
. 15分

练习册系列答案
相关题目
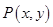 为函数
为函数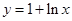 图象上一点,O为坐标原点,记直线
图象上一点,O为坐标原点,记直线 的斜率
的斜率 .
.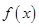 在区间
在区间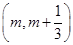
 上存在极值,求实数m的取值范围;
上存在极值,求实数m的取值范围;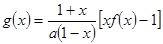 ,若对任意
,若对任意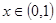 恒有
恒有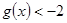 ,求实数
,求实数 的取值范围.
的取值范围.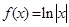
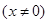 ,函数
,函数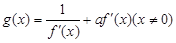
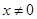 时,求函数
时,求函数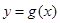 的表达式;
的表达式;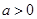 ,函数
,函数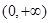 上的最小值是2 ,求
上的最小值是2 ,求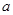 的值.
的值.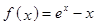 (e为自然对数的底数)
(e为自然对数的底数)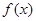 的最小值;
的最小值;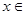
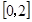 ,不等式
,不等式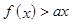 恒成立,求实数
恒成立,求实数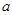 的取值范围.
的取值范围. 。
。 ,求
,求 在
在 处的切线方程;
处的切线方程; 的取值范围。
的取值范围。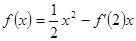 ,
,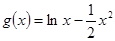 。
。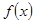 的解析式;
的解析式;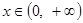 ,都有
,都有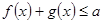 成立,求实数
成立,求实数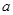 的取值范围;
的取值范围; ,
,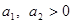 ,且
,且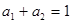 ,求证:
,求证: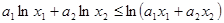 。
。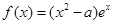 .
.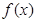 在
在 上不是单调函数,求实数
上不是单调函数,求实数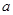 的取值范围;
的取值范围;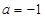 时,讨论函数
时,讨论函数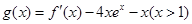 的零点个数.
的零点个数.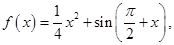
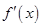 为
为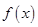 的导函数,则
的导函数,则