题目内容
16.设x,y,z是大于0的实数,则$\frac{xy+yz+zx}{6{x}^{2}+6{y}^{2}+6{z}^{2}}$的最大值是$\frac{1}{6}$.分析 首先利用均值不等式,得到x2+y2+z2≥xy+xz+yz,进而根据不等式的基本性质,得到答案.
解答 解:∵(x-y)2+(x-z)2+(y-z)2≥0,
∴2(x2+y2+z2)≥2(xy+xz+yz),
∴x2+y2+z2≥xy+xz+yz,
∴$\frac{xy+yz+zx}{{x}^{2}+{y}^{2}+{z}^{2}}$≤1,
∴$\frac{xy+yz+zx}{6{x}^{2}+6{y}^{2}+6{z}^{2}}$≤$\frac{1}{6}$,
故$\frac{xy+yz+zx}{6{x}^{2}+6{y}^{2}+6{z}^{2}}$的最大值是$\frac{1}{6}$
故答案为:$\frac{1}{6}$
点评 本题主要考查了基本不等式的应用.基本不等式是解决多项式和函数的最值问题的常用方法,平时应熟练掌握.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
6.有三个房间需要粉刷,粉刷方案要求:每个房间只用一种颜色,且三个房间颜色各不相同.三个房间的粉刷面积和三种颜色的涂料费用如表:
那么在所有不同的粉刷方案中,最低的涂料总费用是1464元.
| 房间A | 房间B | 房间C |
| 35m2 | 20m2 | 28m2 |
| 涂料1 | 涂料2 | 涂料3 |
| 16元/m2 | 18元/m2 | 20元/m2 |
4.执行如图所示的程序框图,输出c的结果为( )
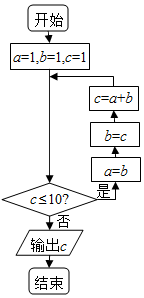

| A. | 13 | B. | 21 | C. | 17 | D. | 15 |
1.若an>0,a1=2,且当n≥2时,有an+an-1=$\frac{n}{{a}_{n}-{a}_{n-1}}$+2,求数列{$\frac{1}{({a}_{n}-1)^{2}}$}的所有项之和.
8.已知函数f(x)=sin(2x+φ)(|φ|<π)的图象过点P(0,$\frac{1}{2}$),如图,则φ的值为( )
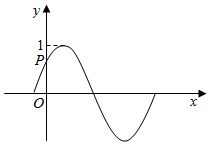

| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{6}$或$\frac{5π}{6}$ | D. | -$\frac{π}{6}$或$\frac{5π}{6}$ |
