题目内容
(本小题满分16分)
已知函数 ,
,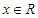 ,
,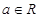 .
.
(1)当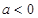 时,若函数
时,若函数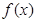 在区间
在区间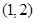 上是单调增函数,试求
上是单调增函数,试求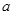 的取值范围;
的取值范围;
(2)当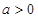 时,直接写出(不需给出演算步骤)函数
时,直接写出(不需给出演算步骤)函数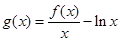 (
(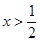 )的单调增区间;
)的单调增区间;
(3)如果存在实数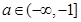 ,使函数
,使函数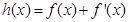 ,
,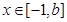 (
(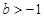 )在
)在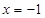 处取得最小值,试求实数
处取得最小值,试求实数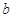 的最大值.
的最大值.
(1)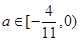 (2)
(2)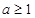 时,增区间
时,增区间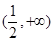 ,
,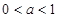 时,减区间
时,减区间 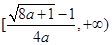 (3)
(3)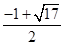
解析试题分析:(1)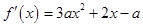
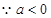 函数
函数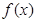 在区间
在区间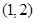 上是单调增函数
上是单调增函数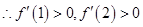
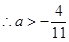
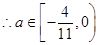
(2)当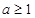 时,
时,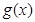 在
在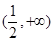 上是增函数;
上是增函数;
当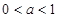 时,
时,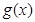 在
在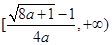 上是增函数.
上是增函数.
(3)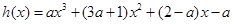 ,
,
根据题意,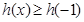 在区间
在区间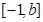 上恒成立,
上恒成立,
即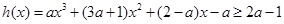 成立
成立
整理得: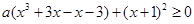 ,
,
即 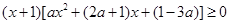 ①
①
当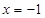 时,不等式①恒成立;
时,不等式①恒成立;
当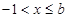 时,不等式①可化为
时,不等式①可化为 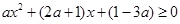 ②
②
令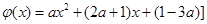 ,
,
根据题设条件,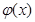 的图象是开口向下的抛物线,故它在闭区间上的最小值必在区间端点取得,又
的图象是开口向下的抛物线,故它在闭区间上的最小值必在区间端点取得,又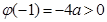 ,所以不等式②恒成立的条件是
,所以不等式②恒成立的条件是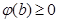
即 ,变量分离得:
,变量分离得: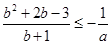 ,③
,③
由条件,存在实数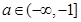 使得③有解,所以
使得③有解,所以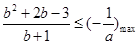 ,
,
即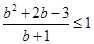 ,整理得
,整理得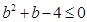 ,解得:
,解得: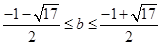
又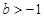 ,所以
,所以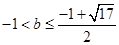 ,即实数
,即实数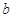 的最大值是
的最大值是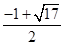 .
.
考点:求函数的单调区间最值
点评:本题第三问难度较大,对于学生没有明显的区分度

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,
, ,
, 所围成的平面图形的面积。
所围成的平面图形的面积。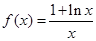 。
。 如果
如果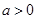 ,函数在区间
,函数在区间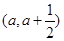 上存在极值,求实数a的取值范围;
上存在极值,求实数a的取值范围; 当
当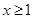 时,不等式
时,不等式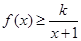 恒成立,求实数k的取值范围。
恒成立,求实数k的取值范围。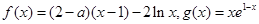 ,(
,(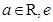 为自然对数的底数)。
为自然对数的底数)。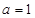 时,求函数
时,求函数 在区间
在区间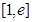 上的最大值和最小值;
上的最大值和最小值; 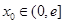 ,在
,在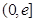 上总存在两个不同的
上总存在两个不同的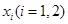 ,使得
,使得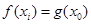 成立,求
成立,求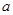 的取值范围。
的取值范围。 .
. 在点
在点 处的切线与直线
处的切线与直线 垂直,求函数
垂直,求函数 都有
都有 成立,试求
成立,试求 的取值范围;
的取值范围; .当
.当 时,函数
时,函数 在区间
在区间 上有两个零点,求实数
上有两个零点,求实数 的取值范围.
的取值范围. ,函数
,函数 的最小值为
的最小值为 ,
, 时,求
时,求 同时满足下列条件:①
同时满足下列条件:① ;②当
;②当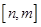 时,值域为
时,值域为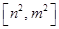
 ?若存在,求出
?若存在,求出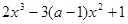 ,其中
,其中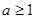
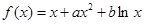 ,曲线
,曲线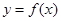 过点
过点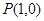 ,且在
,且在 点处的切线斜率为2.
点处的切线斜率为2.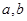 的值;
的值;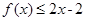
 ,函数
,函数
 .
. 的极值;
的极值; 在
在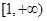 上为单调递增函数,求
上为单调递增函数,求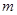 的取值范围;
的取值范围; ,若在
,若在 (
( 是自然对数的底数)上至少存在一个
是自然对数的底数)上至少存在一个 ,使得
,使得 成立,求
成立,求