题目内容
已知函数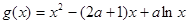
(Ⅰ)当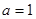 时, 求函数
时, 求函数 的单调增区间;
的单调增区间;
(Ⅱ)求函数 在区间
在区间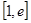 上的最小值;
上的最小值;
(Ⅲ)
在(Ⅰ)的条件下,设 ,
,
证明: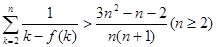 .参考数据:
.参考数据: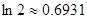 .
.
【答案】
(Ⅰ) (Ⅱ)
(Ⅱ)
(Ⅲ)用放缩法证明.
【解析】
试题分析:(Ⅰ)当 时,
时, ,
,
 或
或 。函数
。函数 的单调增区间为
的单调增区间为
(Ⅱ)  ,
,
当 ,
, 单调增。
单调增。
当 ,
, 单调减.
单调减.  单调增。
单调增。 当
当 ,
, 单调减,
单调减,

(Ⅲ)令 ,
,
 ,
, 
 即
即
 ,
, ,
,




考点:利用导数求闭区间上函数的最值 利用导数研究函数的单调性 不等式的证明
点评:本题考查函数的单调区间和函数的最小值的求法,而利用单调性证明不等式是难题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
 .
. 时,求
时,求 的单调区间;
的单调区间; 单调增加,在
单调增加,在 单调减少,证明:
单调减少,证明: <6.
<6.
 时,求
时,求 的解集
的解集 的不等式
的不等式 的解集是
的解集是 ,求
,求 的取值范围
的取值范围 .
. 时,求
时,求 的极小值;
的极小值; 对任意的
对任意的 都不是曲线
都不是曲线 的切线,求
的切线,求 的取值范围.
的取值范围.

 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;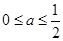 时,讨论
时,讨论 的单调性
的单调性