题目内容
(本题13分)
已知函数 .
.
(1)当 时,求
时,求 的单调区间;
的单调区间;
(2)若 在
在 单调增加,在
单调增加,在 单调减少,证明:
单调减少,证明: <6.
<6.
解:(1)当
 时,
时,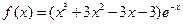 ,故
,故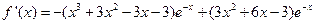
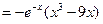
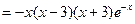
当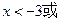
 当
当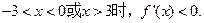
从而 单调减少.----(6分)
单调减少.----(6分)
(2)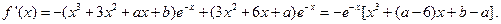
由条件得: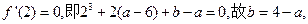
从而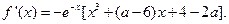
因为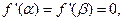
所以
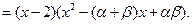
将右边展开,与左边比较系数得,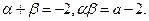
故
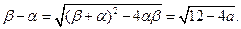
又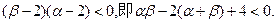
由此可得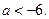 于是
于是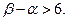 --------------------(13分)
--------------------(13分)
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
(本题13分)
已知函数 .
.
(1)当 时,求
时,求 的单调区间;
的单调区间;
(2)若 在
在 单调增加,在
单调增加,在 单调减少,证明:
单调减少,证明: <6.
<6.
解:(1)当
 时,
时,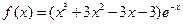 ,故
,故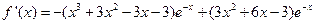
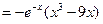
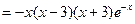
当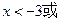
 当
当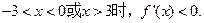
从而 单调减少.----(6分)
单调减少.----(6分)
(2)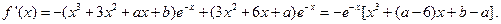
由条件得: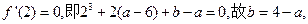
从而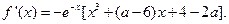
因为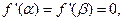
所以
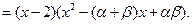
将右边展开,与左边比较系数得,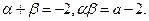
故
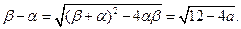
又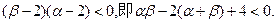
由此可得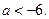 于是
于是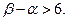 --------------------(13分)
--------------------(13分)
解析

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案