Question

C

Answer 1

（Ⅰ）解：因为，所以,.

因为,所以,.

因为,所以,.

所以.    …………………………………… 2分

由此猜想，当时,，则，.… 3分

下面用数学归纳法证明：

①当时，已证成立.                                            

②假设当（，且）猜想成立，

      即，，.

     当时，由， 得，则，.

 综上所述，猜想成立.

所以.

故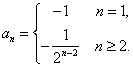.       ……………………………………………… 6分

（Ⅱ）解：当时，假设，根据已知条件则有，

与矛盾，因此不成立，      …………… 7分

所以有，从而有，所以.           

当时，，,

所以;       …………………… 8分

当时，总有成立.

又，

所以数列()是首项为，公比为的等比数列, ，,

又因为，所以.   …………………………… 10分

（Ⅲ）证明：由题意得

                          .

因为，所以.

所以数列是单调递增数列.            …………………………………… 11分

因此要证,只须证.

由，则<，即.…… 12分

因此

.

所以.

故当,恒有.       …………………………………………………14分