Question

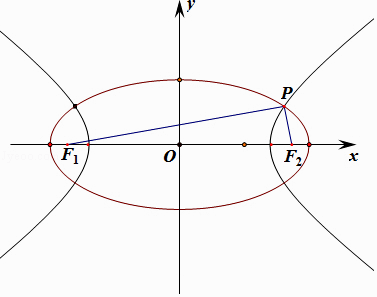
【题目】已知椭圆C1与双曲线C2有相同的左右焦点F1、F2 ， P为椭圆C1与双曲线C2在第一象限内的一个公共点，设椭圆C1与双曲线C2的离心率为e1 ， e2 ， 且 = ，若∠F1PF2= ，则双曲线C2的渐近线方程为（ ）
A.x±y=0
B.x± y=0
C.x± y=0
D.x±2y=0

Answer 1

【答案】C
【解析】解：设椭圆C1的方程： （a1＞b1＞0），双曲线C2的方程： （a2＞0，b2＞0），

焦点F1（﹣c，0），F2（c，0），

由e1= ，e1= ，由 = ，则 = ，则a1=3a2，

由题意的定义：丨PF1丨+丨PF2丨=2a1，丨PF1丨﹣丨PF2丨=2a2，

则丨PF1丨=a1+a2=4a2，丨PF2丨=a1﹣a2=2a2，

由余弦定理可知：丨F1F2丨2=丨PF1丨2+丨PF1丨2﹣2丨PF1丨丨PF1丨cos∠F1PF2，

则（2c）2=（4a2）2+（2a2）2﹣2×4a2×2a2× ，

c2=3a22，b22=c2﹣a22=2a22，则b2= a2，

双曲线的渐近线方程y=± x=± x，即x± y=0，

故选：C．