Question

【题目】已知角x始边与x轴的非负半轴重合，与圆x2+y2=4相交于点A，终边与圆x2+y2=4相交于点B，点B在x轴上的射影为C，△ABC的面积为S（x），函数y=S（x）的图象大致是（ ）
A.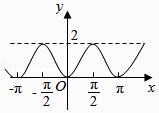
B.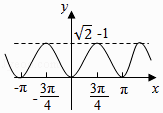
C.
D.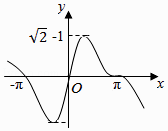

Answer 1

【答案】B
【解析】解：如图A（2，0），在RT△BOC中，

|BC|=2|sinx|，|OC|=2|cosx|，

∴△ABC的面积为S（x）= |BC||AC|≥0，

所以排除C、D；

选项A、B的区别是△ABC的面积为S（x）何时取到最大值？

下面结合选项A、B中的图象利用特值验证：

当x= 时，△ABC的面积为S（x）= =2，

当x= 时，|BC|=2|sin |= ，|OC|=2|cos |= ，

则|AC|=2+ ，

∴△ABC的面积为S（x）= = ，

综上可知，答案B的图象正确，

故选：B．

【考点精析】本题主要考查了直线与圆的三种位置关系的相关知识点，需要掌握直线与圆有三种位置关系：无公共点为相离；有两个公共点为相交,这条直线叫做圆的割线；圆与直线有唯一公共点为相切，这条直线叫做圆的切线，这个唯一的公共点叫做切点才能正确解答此题．