题目内容
已知1≤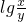 ≤2,2≤
≤2,2≤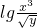 ≤3,则
≤3,则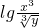 的取值范围是________.
的取值范围是________.

分析:由于1≤
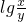 ≤2,2≤
≤2,2≤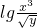 ≤3,则
≤3,则 ,利于线性规划的有关知识来求出
,利于线性规划的有关知识来求出 的范围.
的范围.解答:由于1≤
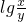 ≤2,2≤
≤2,2≤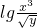 ≤3,则
≤3,则 ,且
,且
若令lgx=a,lgy=b,则问题及转化为求在线性约束
 条件下的
条件下的 的最值问题.
的最值问题.画出可行域,如图中阴影部分所示,

而直线
 上下平移在虚线位置分别取得最值,
上下平移在虚线位置分别取得最值,由
 得到A
得到A ,此时Z=
,此时Z=
由
 得到B(1,0),此时Z=3
得到B(1,0),此时Z=3则
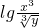 的取值范围是
的取值范围是 ,
,故答案为

点评:本题主要考查了对数的运算性质以及线性规划,熟记一些常用的结论可以简化基本运算.

练习册系列答案
相关题目