已知椭圆的方程为$\frac{{y}^{2}}{25}$+$\frac{{x}^{2}}{16}$=1.则椭圆的长轴长为( )A．4B．5C．10D．8 题目和参考答案——青夏教育精英家教网—

题目内容

20．已知椭圆的方程为$\frac{{y}^{2}}{25}$+$\frac{{x}^{2}}{16}$=1，则椭圆的长轴长为（　　）

A．

B．

C．

D．

分析求得椭圆的a=5，可得长轴长为2a=10．

解答解：椭圆的方程为$\frac{{y}^{2}}{25}$+$\frac{{x}^{2}}{16}$=1，
可得椭圆的焦点在y轴上，
即有a=5，可得椭圆的长轴长为2a=10．
故选：C．

点评本题考查椭圆的方程和性质，考查长轴长的求法，属于基础题．

练习册系列答案

相关题目

10．

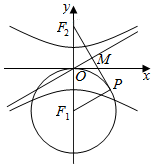如图，已知F₁，F₂是双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1\;（a＞0，b＞0）$的下，上焦点，过F₂点作以F₁为圆心，|OF₁|为半径的圆的切线，P为切点，若切线段PF₂被一条渐近线平分，则双曲线的离心率为（　　）

11．若经过点（3，a）、（-2，0）的直线与经过点（3，-4）且斜率为$\frac{1}{2}$的直线垂直，则a的值为-10．

8．广丰一中现有职工180人，其中高级职称42人，中级职称78人，一般职员60人，现抽取30人进行分层抽样，则各职称人数分别为（　　）

15．已知f（x）=$\frac{x-a}{{{x^2}+1}}$是奇函数，g（x）=x²+bx+1为偶函数．
（1）求a，b的值；
（2）对任意x∈R不等式2f（x）g（x）＜g（x）-m恒成立，求m的取值范围．

5．已知递增的等差数列{a_n}中，a₂、a₅是方程x²-12x+27=0的两根，数列{b_n}的前n项和为S_n，且S_n=1-$\frac{1}{2}{b_n}（{n∈{N^*}}）$．
（1）求数列{a_n}，{b_n}的通项公式；
（2）记c_n=a_n•b_n，数列{c_n}的前n项和为T_n．求证：T_n＜2．

12．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，且短轴长为2，O为坐标原点．
（1）求椭圆的标准方程；
（2）设直线l：y=kx+$\sqrt{2}$与椭圆交于A、B两点，且$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\frac{2}{3}$，求k的值．

9．在△ABC中，∠CAB=∠CBA=30°，AC，BC边上的高分别为BD，AE，则以A，B为焦点，且过D，E两点的椭圆离心率为（　　）

10．椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左焦点为F₁，右焦点为F₂，离心率e=$\frac{1}{2}$．过F₁的直线交椭圆于A，B两点，且△ABF₂的周长为8．
（1）求椭圆E的方程．
（2）在椭圆E上，是否存在点M（m，n）使得直线l：mx+ny=1与圆O：x²+y²=1相交于不同的两点P，Q，且△POQ的面积最大？若存在，求出点M的坐标及相对应的△POQ的面积；若不存在，请说明理由．

试题分类