题目内容
已知函数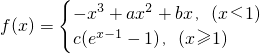 在
在 处存在极值.
处存在极值.
(1)求实数a,b的值;
(2)函数y=f(x)的图象上存在两点A,B使得△AOB是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在y轴上,求实数c的取值范围;
(3)当c=e时,讨论关于x的方程f(x)=kx(k∈R)的实根的个数.
解(1)当x<1时,f′(x)=-3x2+2ax+b.(1分)
因为函数f(x)在x=0,x= 处存在极值,所以
处存在极值,所以 解得a=1,b=0.(3分)
解得a=1,b=0.(3分)
(2)由(1)得f(x)= ,
,
根据条件知A,B的横坐标互为相反数,不妨设A(-t,t3+t2),B(t,f(t)),(t>0).
若t<1,则f(t)=-t3+t2,
由∠AOB是直角得, •
• =0,即-t2+(t3+t2)(-t3+t2)=0,
=0,即-t2+(t3+t2)(-t3+t2)=0,
即t4-t2+1=0.此时无解; (5分)
若t≥1,则f(t)=c(et-1-1).由于AB的中点在y轴上,且∠AOB是直角,所以B点不可能在x轴上,即t≠1.
由 •
• =0,即-t2+(t3+t2)•c(et-1-1)=0,得c=
=0,即-t2+(t3+t2)•c(et-1-1)=0,得c= .
.
因为函数y=(t+1)(et-1-1)在t>1上的值域是(0,+∞),
所以实数c的取值范围是(0,+∞).(7分)
(3)由方程f(x)=kx,知kx= ,可知0一定是方程的根,(8分)
,可知0一定是方程的根,(8分)
所以仅就x≠0时进行研究:方程等价于k= ,
,
构造函数g(x)= ,
,
对于x<1且x≠0部分,函数g(x)=-x2+x的图象是开口向下的抛物线的一部分,
当x= 时取得最大值
时取得最大值 ,其值域是(-∞,0)∪(0,
,其值域是(-∞,0)∪(0, );
);
对于x≥1部分,函数g(x)= ,由g′(x)=
,由g′(x)= >0,知函数g(x)在(1,+∞)上单调递增.
>0,知函数g(x)在(1,+∞)上单调递增.
所以,①当k> 或k≤0时,方程f(x)=kx有两个实根;
或k≤0时,方程f(x)=kx有两个实根;
②当k= 时,方程f(x)=kx有三个实根;
时,方程f(x)=kx有三个实根;
③当0<k< 时,方程f(x)=kx有四个实根.(14分)
时,方程f(x)=kx有四个实根.(14分)
分析:(1)当x<1时,f′(x)=-3x2+2ax+b,依题意,由 可求实数a,b的值;
可求实数a,b的值;
(2)由(1)可求得f(x)= ,依题意A,B的横坐标互为相反数,不妨设A(-t,t3+t2),B(t,f(t)),(t>0).分t<1与t≥1讨论,利用∠AOB是直角,
,依题意A,B的横坐标互为相反数,不妨设A(-t,t3+t2),B(t,f(t)),(t>0).分t<1与t≥1讨论,利用∠AOB是直角, •
• =0,即可求得实数c的取值范围;
=0,即可求得实数c的取值范围;
(3)由方程f(x)=kx,知kx= ,可知0一定是方程的根,x≠0,方程等价于k=
,可知0一定是方程的根,x≠0,方程等价于k= ,构造函数g(x)=
,构造函数g(x)= ,
,
分x<1且x≠0与x≥1两类讨论,即可确定f(x)=kx(k∈R)的实根的个数.
点评:本题考查利用导数研究函数的极值,考查根的存在性及根的个数判断,突出分类讨论思想、等价转化思想及创新思维与逻辑思维能力的考查,属于难题.
因为函数f(x)在x=0,x=
 处存在极值,所以
处存在极值,所以 解得a=1,b=0.(3分)
解得a=1,b=0.(3分)(2)由(1)得f(x)=
 ,
,根据条件知A,B的横坐标互为相反数,不妨设A(-t,t3+t2),B(t,f(t)),(t>0).
若t<1,则f(t)=-t3+t2,
由∠AOB是直角得,
 •
• =0,即-t2+(t3+t2)(-t3+t2)=0,
=0,即-t2+(t3+t2)(-t3+t2)=0,即t4-t2+1=0.此时无解; (5分)
若t≥1,则f(t)=c(et-1-1).由于AB的中点在y轴上,且∠AOB是直角,所以B点不可能在x轴上,即t≠1.
由
 •
• =0,即-t2+(t3+t2)•c(et-1-1)=0,得c=
=0,即-t2+(t3+t2)•c(et-1-1)=0,得c= .
.因为函数y=(t+1)(et-1-1)在t>1上的值域是(0,+∞),
所以实数c的取值范围是(0,+∞).(7分)
(3)由方程f(x)=kx,知kx=
 ,可知0一定是方程的根,(8分)
,可知0一定是方程的根,(8分)所以仅就x≠0时进行研究:方程等价于k=
 ,
,构造函数g(x)=
 ,
,对于x<1且x≠0部分,函数g(x)=-x2+x的图象是开口向下的抛物线的一部分,
当x=
 时取得最大值
时取得最大值 ,其值域是(-∞,0)∪(0,
,其值域是(-∞,0)∪(0, );
);对于x≥1部分,函数g(x)=
 ,由g′(x)=
,由g′(x)= >0,知函数g(x)在(1,+∞)上单调递增.
>0,知函数g(x)在(1,+∞)上单调递增.所以,①当k>
 或k≤0时,方程f(x)=kx有两个实根;
或k≤0时,方程f(x)=kx有两个实根;②当k=
 时,方程f(x)=kx有三个实根;
时,方程f(x)=kx有三个实根;③当0<k<
 时,方程f(x)=kx有四个实根.(14分)
时,方程f(x)=kx有四个实根.(14分)分析:(1)当x<1时,f′(x)=-3x2+2ax+b,依题意,由
 可求实数a,b的值;
可求实数a,b的值;(2)由(1)可求得f(x)=
 ,依题意A,B的横坐标互为相反数,不妨设A(-t,t3+t2),B(t,f(t)),(t>0).分t<1与t≥1讨论,利用∠AOB是直角,
,依题意A,B的横坐标互为相反数,不妨设A(-t,t3+t2),B(t,f(t)),(t>0).分t<1与t≥1讨论,利用∠AOB是直角, •
• =0,即可求得实数c的取值范围;
=0,即可求得实数c的取值范围;(3)由方程f(x)=kx,知kx=
 ,可知0一定是方程的根,x≠0,方程等价于k=
,可知0一定是方程的根,x≠0,方程等价于k= ,构造函数g(x)=
,构造函数g(x)= ,
,分x<1且x≠0与x≥1两类讨论,即可确定f(x)=kx(k∈R)的实根的个数.
点评:本题考查利用导数研究函数的极值,考查根的存在性及根的个数判断,突出分类讨论思想、等价转化思想及创新思维与逻辑思维能力的考查,属于难题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
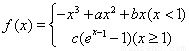
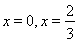
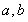
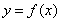
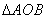
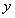
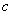
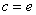
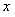

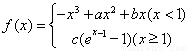
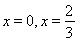
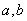
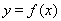


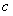
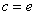
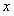

 在
在 处取得极值.
处取得极值. ;
;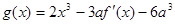 ,如果
,如果 在开区间
在开区间 上存在极小值,求实数
上存在极小值,求实数 的取值范围.
的取值范围.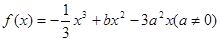 在
在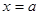 处取得极值.
处取得极值.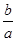 ;
;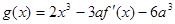 ,如果
,如果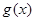 在开区间
在开区间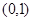 上存在极小值,求实数
上存在极小值,求实数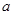 的取值范围.
的取值范围.