题目内容
【题目】如图,在四棱锥![]() ,
,![]() 为矩形,
为矩形,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() .
.
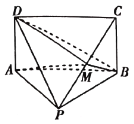
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 为
为![]() 中点,直线
中点,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的正弦值.
的正弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)推导出![]() 平面
平面![]() ,
,![]() ,从而
,从而![]() 平面
平面![]() ,由此能证明平面
,由此能证明平面![]() 平面
平面![]() .
.
(2)由![]() 平面
平面![]() ,
,![]() 为
为![]() 在平面
在平面![]() 内的射影,从而
内的射影,从而![]() 即为直线
即为直线![]() 与平面
与平面![]() 所成的角,取
所成的角,取![]() 中点
中点![]() ,连结
,连结![]() ,则
,则![]() ,以
,以![]() 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系![]() ,利用向量法能求出二面角
,利用向量法能求出二面角![]() 的正弦值.
的正弦值.
(1)证明:∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
矩形![]() 中,
中,![]() ,
,
∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,
∴![]() .
.
又∵![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(2)解:由(1)知![]() 平面
平面![]() ,
,![]() 为
为![]() 在平面
在平面![]() 内的射影,
内的射影,
∴![]() 即为直线
即为直线![]() 与平面
与平面![]() 所成的角,
所成的角,
由题意,![]() ,
,![]() ,
,
取![]() 中点
中点![]() ,连结
,连结![]() ,则
,则![]() ,
,
以![]() 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系![]() ,
,
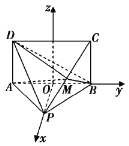
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
则![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则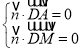 ,即
,即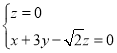 ,
,
令![]() ,则
,则![]() ,
,![]() ,∴
,∴![]() .
.
同理易得,平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由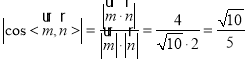 ,
,
∴二面角![]() 的正弦值为
的正弦值为![]() .
.

【题目】随着科技的发展,网购已经逐渐融入了人们的生活,在家里不用出门就可以买到自己想要的东西,在网上付款即可,两三天就会送到自己的家门口,所以选择网购的人数在逐年增加.某网店统计了2014年一2018年五年来在该网店的购买人数![]() (单位:人)各年份的数据如下表:
(单位:人)各年份的数据如下表:
年份( | 1 | 2 | 3 | 4 | 5 |
| 24 | 27 | 41 | 64 | 79 |
(1)依据表中给出的数据,是否可用线性回归模型拟合![]() 与时间
与时间![]() (单位:年)的关系,请通过计算相关系数
(单位:年)的关系,请通过计算相关系数![]() 加以说明,(若
加以说明,(若![]() ,则该线性相关程度很高,可用线性回归模型拟合)
,则该线性相关程度很高,可用线性回归模型拟合)
附:相关系数公式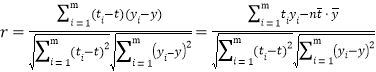
参考数据![]()
![]()
![]()
![]()
(2)该网店为了更好的设计2019年的“双十一”网购活动安排,统计了2018年“双十一”期间8个不同地区的网购顾客用于网购的时间x(单位:小时)作为样本,得到下表
地区 |
|
|
|
|
|
|
|
|
时间 | 0.9 | 1.6 | 1.4 | 2.5 | 2.6 | 2.4 | 3.1 | 1.5 |
①求该样本数据的平均数![]() ;
;
②通过大量数据统计发现,该活动期间网购时间![]() 近似服从正态分布
近似服从正态分布![]() ,如果预计2019年“双十一”期间的网购人数大约为50000人,估计网购时间
,如果预计2019年“双十一”期间的网购人数大约为50000人,估计网购时间![]() 的人数.
的人数.
(附:若随机变量![]() 服从正态分布
服从正态分布![]() 则
则![]() ,
,![]()