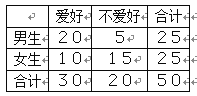
题目内容
【题目】已知如图,长方体![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点,过点
的中点,过点![]() 的平面
的平面![]() 与平面
与平面![]() 平行,且与长方体的面相交,交线围成一个几何图形.
平行,且与长方体的面相交,交线围成一个几何图形.
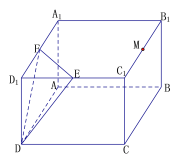
(1)在图中画出这个几何图形,并求这个几何图形的面积(画图说出作法,不用说明理由);
(2)求证:![]() 平面
平面![]() .
.
【答案】(1) ![]() .(2)见解析.
.(2)见解析.
【解析】
(1)以公理三及其推理,以及面面平行判定定理为依据,即可作出过点![]() 且与平面
且与平面![]() 平行的平面
平行的平面![]() ,由于其截面为等腰梯形,对应运用梯形面积公式即可求出该梯形面积.
,由于其截面为等腰梯形,对应运用梯形面积公式即可求出该梯形面积.
(2)设![]() 交EF于Q,连接DQ,关键通过证明
交EF于Q,连接DQ,关键通过证明![]() 以及
以及![]() ,即可利用线面垂直判定定理证明.而对于
,即可利用线面垂直判定定理证明.而对于![]() 的证明,可以通过
的证明,可以通过![]() 平面
平面![]() 即可,而
即可,而![]() 的证明,需要证得
的证明,需要证得![]() 即可.
即可.
(1)设N为![]() 的中点,连结MN,AN、AC、CM,
的中点,连结MN,AN、AC、CM,
则四边形MNAC为所作图形;
易知MN![]() (或
(或![]() ),四边形
),四边形![]() 为梯形,
为梯形,
且![]() ,
,
过M作MP⊥AC于点P,可得![]() ,
,
![]() ,得
,得![]()
所以梯形![]() 的面积=
的面积=![]() ;
;
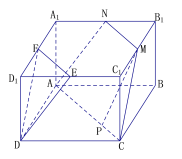
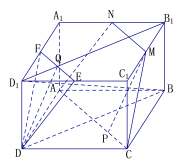
(2)证法1:在长方体中![]() ,设
,设![]() 交EF于Q,连接DQ,则Q为EF的中点并且为
交EF于Q,连接DQ,则Q为EF的中点并且为![]() 的四等点,如图,
的四等点,如图,![]()
由![]() 得
得![]() ,又
,又![]() ,
,![]() ,
,
![]() 平面
平面![]() ,则
,则![]() ,
,
![]() 且
且![]() ,则
,则![]()
![]()
![]() ,
,
![]() ,
,
![]() 平面
平面![]()
证法2:设![]() 交EF于Q,连接DQ,则Q为EF的中点,且为
交EF于Q,连接DQ,则Q为EF的中点,且为![]() 的四等分点,
的四等分点,
![]()
由![]() 可知
可知![]() ,
,
又![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]()
由![]() 得
得![]() ,
,
得![]() ,
,
![]() ,
,
![]() ,又
,又![]() ,
,
![]() 平面
平面![]()

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目