题目内容
9、如图，两个正方形ABCD和ADEF所在平面互相垂直，设M、N分别是BD和AE的中点，那么①AD⊥MN；②MN∥面CDE；③MN∥CE；④MN、CE异面其中正确结论的序号是①②③
．分析：取AD的中点G，连接MG，NG，结合正方形的性质，我们结合线面垂直的判定定理及性质可判断①的真假；连接AC，CE，根据三角形中位线定理，及线面平行的判定定理，可以判断②③④的真假，进而得到答案．
解答：解：∵两个正方形ABCD和ADEF所在平面互相垂直，设M、N分别是BD和AE的中点，
取AD的中点G，连接MG，NG，易得AD⊥平面MNG，进而得到AD⊥MN，故①正确；
连接AC，CE，根据三角形中位线定理，可得MN∥CE，由线面平行的判定定理，可得②MN∥面CDE及③MN∥CE正确，④MN、CE错误；
故答案为：①②③．
∵两个正方形ABCD和ADEF所在平面互相垂直，设M、N分别是BD和AE的中点，取AD的中点G，连接MG，NG，易得AD⊥平面MNG，进而得到AD⊥MN，故①正确；
连接AC，CE，根据三角形中位线定理，可得MN∥CE，由线面平行的判定定理，可得②MN∥面CDE及③MN∥CE正确，④MN、CE错误；
故答案为：①②③．
点评：本题考查的知识点是平面与平面垂直的性质，直线与平面垂直的判定及直线与平面平行的判定，熟练掌握空间直线与平面平行及垂直的判定及性质是解答本题的关键．
练习册系列答案
相关题目
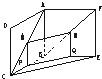如图，两个全等的正方形ABCD和ABEF所在平面相交于AB，M∈AC，N∈FB且AM=FN，求证：MN∥平面BCE．
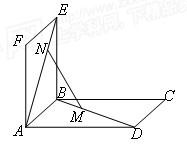如图，两个边长为1的正方形ABCD与ABEF相交于AB，∠EBC=90°，M，N分别是BD，AE上的点，且AN=DM．
