题目内容
如图,两个全等的正方形ABCD和ABEF所在平面相交于AB,M∈AC,N∈FB且AM=FN,求证:MN∥平面BCE.
证法一:过M作MP⊥BC,NQ⊥BE,P、Q为垂足,连结PQ.
∵MP∥AB,NQ∥AB,
∴MP∥NQ.
又NQ=![]() BN=
BN=![]() CM=MP,
CM=MP,
∴MPQN是平行四边形.∴MN∥PQ,PQ![]() 平面BCE.
平面BCE.
而MN![]() 平面BCE,
平面BCE,
∴MN∥平面BCE.
证法二:过M作MG∥BC,交AB于点G(如图),连结NG.

∵MG∥BC,BC![]() 平面BCE,
平面BCE,
MG![]() 平面BCE,∴MG∥平面BCE.
平面BCE,∴MG∥平面BCE.
又![]() =
=![]() =
=![]() ,∴GN∥AF∥BE,同样可证明GN∥平面BCE.
,∴GN∥AF∥BE,同样可证明GN∥平面BCE.
又MG∩NG=G,
∴平面MNG∥平面BCE.又MN![]() 平面MNG,
平面MNG,
∴MN∥平面BCE.

练习册系列答案
相关题目
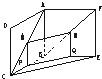 如图,两个全等的正方形ABCD和ABEF所在平面相交于AB,M∈AC,N∈FB且AM=FN,求证:MN∥平面BCE.
如图,两个全等的正方形ABCD和ABEF所在平面相交于AB,M∈AC,N∈FB且AM=FN,求证:MN∥平面BCE. ,
, ,且AM=FN.求证:MN∥平面BCE.
,且AM=FN.求证:MN∥平面BCE.
 ,
, ,且AM=FN.求证:MN∥平面BCE.
,且AM=FN.求证:MN∥平面BCE.

