题目内容
如图,两个边长为1的正方形ABCD与ABEF相交于AB,∠EBC=90°,M,N分别是BD,AE上的点,且AN=DM.(1)求证:MN∥平面EBC;
(2)求MN长度的最小值.

【答案】分析:(1)首先分别以BA,BC,BE为x轴,y轴,z轴建立空间直角坐标系,然后确定点M、N的坐标,进而确定 的坐标,再找到平面EBC的一个法向量
的坐标,再找到平面EBC的一个法向量 ,并确定它的坐标,最后计算
,并确定它的坐标,最后计算 为0即可.
为0即可.
(2)由 的坐标表示出其长度,再利用配方法即可求出它的最小值.
的坐标表示出其长度,再利用配方法即可求出它的最小值.
解答: (1)证明:依题意可分别以BA,BC,BE为x轴,y轴,z轴建立;
(1)证明:依题意可分别以BA,BC,BE为x轴,y轴,z轴建立;
如图所示空间直角坐标系,
因为正方形ABCD与ABEF的边长为1,且AN=DM,
所以设BM=x,则NE=x,NA= -x,且x
-x,且x ,
,
所以M( x,
x, x,0),N(
x,0),N( x,0,1-
x,0,1- x),
x),
所以 =(0,-
=(0,- x,1-
x,1- x),
x),
因为平面EBC的一个法向量为 =(1,0,0)
=(1,0,0)
所以 =0,即
=0,即 ,
,
又MN?平面EBC,所以MN∥平面EBC.
(2)解:由(1) =(0,-
=(0,- x,1-
x,1- x),得
x),得
| |=
|= =
= ,
,
又x∈[0, ],所以当x=
],所以当x= 时,|
时,| |min=
|min= .
.
即MN长度的最小值为 .
.
点评:本题主要考查向量法解决立体几何问题.
 的坐标,再找到平面EBC的一个法向量
的坐标,再找到平面EBC的一个法向量 ,并确定它的坐标,最后计算
,并确定它的坐标,最后计算 为0即可.
为0即可.(2)由
 的坐标表示出其长度,再利用配方法即可求出它的最小值.
的坐标表示出其长度,再利用配方法即可求出它的最小值.解答:
 (1)证明:依题意可分别以BA,BC,BE为x轴,y轴,z轴建立;
(1)证明:依题意可分别以BA,BC,BE为x轴,y轴,z轴建立;如图所示空间直角坐标系,
因为正方形ABCD与ABEF的边长为1,且AN=DM,
所以设BM=x,则NE=x,NA=
 -x,且x
-x,且x ,
,所以M(
 x,
x, x,0),N(
x,0),N( x,0,1-
x,0,1- x),
x),所以
 =(0,-
=(0,- x,1-
x,1- x),
x),因为平面EBC的一个法向量为
 =(1,0,0)
=(1,0,0)所以
 =0,即
=0,即 ,
,又MN?平面EBC,所以MN∥平面EBC.
(2)解:由(1)
 =(0,-
=(0,- x,1-
x,1- x),得
x),得|
 |=
|= =
= ,
,又x∈[0,
 ],所以当x=
],所以当x= 时,|
时,| |min=
|min= .
.即MN长度的最小值为
 .
.点评:本题主要考查向量法解决立体几何问题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
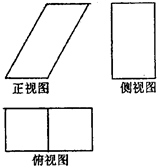 一个几何体的三视图如右图所示.已知正视图是底边长为1的平行四边形,侧视图是一个长为
一个几何体的三视图如右图所示.已知正视图是底边长为1的平行四边形,侧视图是一个长为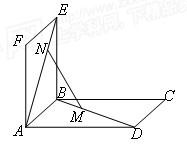 如图,两个边长为1的正方形ABCD与ABEF相交于AB,∠EBC=90°,M,N分别是BD,AE上的点,且AN=DM.
如图,两个边长为1的正方形ABCD与ABEF相交于AB,∠EBC=90°,M,N分别是BD,AE上的点,且AN=DM. 某同学为研究函数
某同学为研究函数 (2012•海淀区二模)某同学为研究函数
(2012•海淀区二模)某同学为研究函数