题目内容
如图，已知| GA |
| GB |
| GC |
| 0 |
| 3 |
分析：根据
+
+
=
，可得G为三角形重心，证明四边形GBEC为平行四边形，然后再利用正弦定理求出GA、GC的长；
| GA |
| GB |
| GC |
| 0 |
解答：解：因为
+
+
=
，所以点G为△ABC的重心，取BC的中点，连接GD，并延长GD到点E，
GD=GE，连接BE，CE，所以四边形GBEC为平行四边形，
∠EGB=45°，∠GEB=60°，所以∠GBE=75°，
在△BGE中，由正弦定理得
=
=
，
所以BE=2
，GE=
+
，
所以GC=2
，GA=
+
；
| GA |
| GB |
| GC |
| 0 |
GD=GE，连接BE，CE，所以四边形GBEC为平行四边形，
∠EGB=45°，∠GEB=60°，所以∠GBE=75°，
在△BGE中，由正弦定理得
2
| ||
| sin60° |
| BE |
| sin45° |
| GE |
| sin75° |
所以BE=2
| 2 |
| 2 |
| 6 |
所以GC=2
| 2 |
| 2 |
| 6 |
点评：此题考查了向量在集合中的应用及正弦定理的应用，解决此题的关键是要会添加辅助线，此题是一道中档题；
练习册系列答案
计算高手系列答案
相关题目
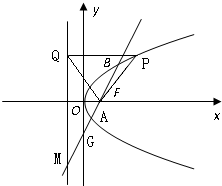如图，已知抛物线y2=2px（p＞0），焦点为F，准线为直线l，P为抛物线上的一点，过点P作l的垂线，垂足为点Q．当P的横坐标为3时，△PQF为等边三角形．
（2012•九江一模）已知点G是△ABC的外心，
（理）如图所示，已知圆C：（x+1）2+y2=8，定点A（1，0），M为圆上一动点，点P在AM上，点N在CM上，且满足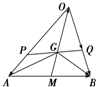
如图所示，已知点G是△ABO的重心．