题目内容
(本小题14分)
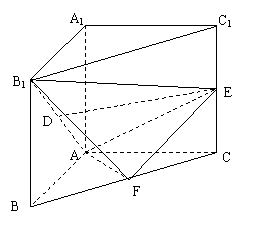
已知直三棱柱![]() 中,
中,![]() 为等腰直角三角形,且
为等腰直角三角形,且![]() ,
,
 且
且![]() ,
,![]() 分别为
分别为![]() 的中点.
的中点.
(Ⅰ)求证:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)求二面角![]() 的大小.
的大小.
解:(Ⅰ)设![]() 的中点为
的中点为![]() ,连接
,连接![]()
∵![]() 是
是![]() 的中点∴
的中点∴![]() ∥
∥![]() 且
且![]()
![]()
∵![]() 是
是![]() 的中点∴
的中点∴![]() ∥
∥![]() 且
且![]()
![]()
∴![]() ∥
∥![]() 且
且![]()
![]()
∴![]() 是平行四边形
是平行四边形
∴![]() ∥
∥![]()
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() ∥平面
∥平面![]() ………………………………………… 4分
………………………………………… 4分
(Ⅱ) ∵ ![]() 为等腰直角三角形,
为等腰直角三角形, ![]() ,且
,且![]() 是
是![]() 的中点
的中点
∴ ![]() ∵平面
∵平面![]() 平面
平面![]()
∴ ![]() 平面
平面![]() ∴
∴![]()
![]() …… 6分
…… 6分
设![]()
则在![]() 中,
中,![]() ,
,
则![]() ,
,![]() ∴
∴![]()
∴ ![]() 是直角三角形,∴
是直角三角形,∴![]() ……………………… 8分
……………………… 8分
∵![]() ∴
∴![]() 平面
平面![]() ……………… 9分
……………… 9分
(Ⅲ)分别以![]() 为
为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() 如图,
如图,
设![]() ,则设
,则设![]() ,
,![]()
∵ ![]() 平面
平面![]()
∴ 面![]() 的法向量为
的法向量为![]() =
=![]() ……………………… 10分
……………………… 10分
设平面![]() 的法向量为
的法向量为![]()
∵ ![]() ,
, ![]()
∴![]() ,
, ![]()
∴![]() ,
,![]()
不妨设![]() ,可得
,可得![]() …………………………… 12分
…………………………… 12分
∴ 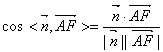 =
=![]() …………………… 13分
…………………… 13分
∵ 二面角![]() 是锐角
是锐角
∴ 二面角![]() 的大小
的大小![]() ………………………… 14分
………………………… 14分

练习册系列答案
相关题目
 .
. ,点P为曲线
,点P为曲线 上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程;
上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程; 上为单调增函数,试求
上为单调增函数,试求 的取值范围.
的取值范围. 满足:
满足: ,
, ,且该函数的最小值为1.
,且该函数的最小值为1. =
=  .(其中
.(其中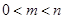 ). 问是否存在这样的两个实数
). 问是否存在这样的两个实数 ,使得函数
,使得函数
 且函数
且函数 在区间
在区间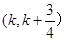 上存在极值,求实数
上存在极值,求实数 的取值范围;
的取值范围; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,
, ……
…… .
. ,x∈[1,+∞
,x∈[1,+∞
 时,求函数f(x)的最小值
时,求函数f(x)的最小值 
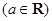 .
. ,求曲线
,求曲线 在
在 处切线的斜率;
处切线的斜率; 的单调区间;
的单调区间; ,若对任意
,若对任意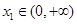 ,均存在
,均存在 ,使得
,使得 ,求
,求 的取值范围。
的取值范围。