题目内容
(本小题满分12分)
对于定义在区间D上的函数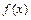 ,若存在闭区间
,若存在闭区间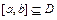 和常数
和常数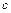 ,使得对任意
,使得对任意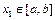 ,都有
,都有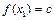 ,
,
且对任意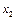 ∈D,当
∈D,当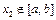 时,
时,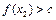 恒成立,则称函数
恒成立,则称函数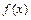 为区间D上的“平底型”函数.
为区间D上的“平底型”函数.
(Ⅰ)判断函数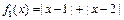 和
和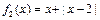 是否为R上的“平底型”函数?并说明理由;
是否为R上的“平底型”函数?并说明理由;

对于定义在区间D上的函数
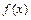 ,若存在闭区间
,若存在闭区间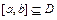 和常数
和常数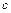 ,使得对任意
,使得对任意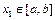 ,都有
,都有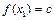 ,
,且对任意
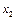 ∈D,当
∈D,当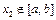 时,
时,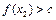 恒成立,则称函数
恒成立,则称函数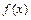 为区间D上的“平底型”函数.
为区间D上的“平底型”函数.(Ⅰ)判断函数
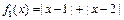 和
和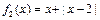 是否为R上的“平底型”函数?并说明理由;
是否为R上的“平底型”函数?并说明理由;
解:(Ⅰ)对于函数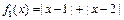 ,当
,当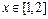 时,
时,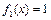 .
.
当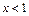 或
或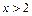 时,
时,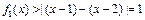 恒成立,故
恒成立,故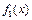 是“平底型”函数.…2分
是“平底型”函数.…2分
对于函数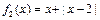 ,当
,当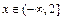
 时,
时,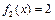 ;
;
当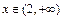 时,
时,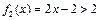 ,所以不存在闭区间
,所以不存在闭区间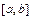 ,使当
,使当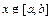 时,
时,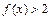 恒成立.
恒成立.
故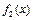 不是“平底型”函数.
不是“平底型”函数.  …4分
…4分
(Ⅱ)若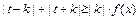 对一切
对一切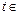 R恒成立,则
R恒成立,则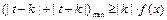 .
.
因为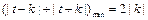 ,所以
,所以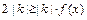 .又
.又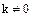 ,则
,则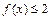 .
.
因为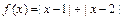 ,则
,则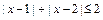 ,解得
,解得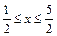 .
.
故实数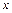 的范围是
的范围是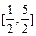 . …7分
. …7分
(Ⅲ)因为函数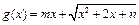 是区间
是区间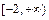 上的“平底型”函数,则
上的“平底型”函数,则
存在区间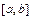
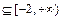 和常数
和常数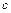 ,使得
,使得 恒成立.
恒成立.
所以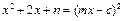 恒成立,即
恒成立,即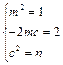 .解得
.解得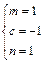 或
或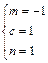 .…9分
.…9分
当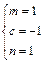 时,
时,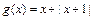 .
.
当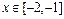 时,
时,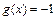 ,当
,当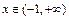 时,
时,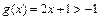 恒成立.
恒成立.
此时,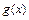 是区间
是区间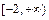 上的“平底型”函数.
上的“平底型”函数.

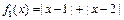 ,当
,当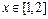 时,
时,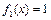 .
.当
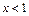 或
或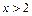 时,
时,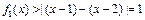 恒成立,故
恒成立,故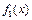 是“平底型”函数.…2分
是“平底型”函数.…2分对于函数
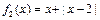 ,当
,当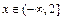
 时,
时,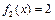 ;
;当
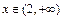 时,
时,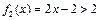 ,所以不存在闭区间
,所以不存在闭区间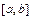 ,使当
,使当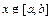 时,
时,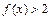 恒成立.
恒成立.故
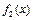 不是“平底型”函数.
不是“平底型”函数.  …4分
…4分(Ⅱ)若
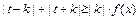 对一切
对一切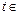 R恒成立,则
R恒成立,则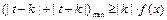 .
.因为
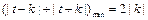 ,所以
,所以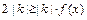 .又
.又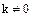 ,则
,则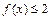 .
. 因为
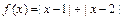 ,则
,则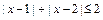 ,解得
,解得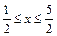 .
.故实数
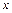 的范围是
的范围是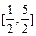 . …7分
. …7分(Ⅲ)因为函数
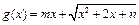 是区间
是区间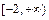 上的“平底型”函数,则
上的“平底型”函数,则存在区间
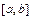
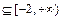 和常数
和常数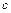 ,使得
,使得 恒成立.
恒成立.所以
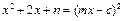 恒成立,即
恒成立,即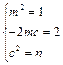 .解得
.解得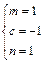 或
或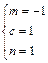 .…9分
.…9分当
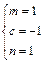 时,
时,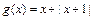 .
.当
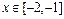 时,
时,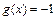 ,当
,当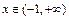 时,
时,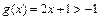 恒成立.
恒成立.此时,
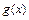 是区间
是区间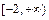 上的“平底型”函数.
上的“平底型”函数. 
略

练习册系列答案
相关题目
 和
和 ,函数
,函数 在闭区间
在闭区间 上的最大值称为
上的最大值称为 则
则 .
. 


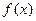 是定义在
是定义在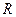 上的以3为周期的偶函数,且
上的以3为周期的偶函数,且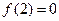 ,则方程
,则方程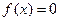 在区
在区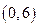 内解的个数的最小值是:
内解的个数的最小值是: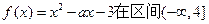 上单调递减,则实数
上单调递减,则实数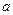 满足的条件是( )
满足的条件是( )



 ,其图像与直线
,其图像与直线 有两个不同的交点,则a的取值范围_
有两个不同的交点,则a的取值范围_ 
 的最小值为
的最小值为 .
.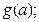
 求
求 及此时
及此时 的最大值.(12分)
的最大值.(12分) 是
是 上的奇函数,且
上的奇函数,且 ,当
,当 时,
时, ,则
,则 ="( " )
="( " )