题目内容
设函数f(x)=lg(|x+3|+|x-7|)-a.
(1)当a=1时,解关于x的不等式f(x)>0;
(2)如果?x∈R,f(x)>0,求a的取值范围.
(1)当a=1时,解关于x的不等式f(x)>0;
(2)如果?x∈R,f(x)>0,求a的取值范围.
考点:对数函数图象与性质的综合应用,绝对值不等式的解法
专题:函数的性质及应用
分析:(1)当a=1时,原不等式可变为|x+3|+|x-7|>10,由绝对值的意义求得其解集.
(2)根据|x+3|+|x-7|≥10对任意x∈R都成立,可得f(x)=lg(|x+3|+|x-7|)-a>0的解集为R,∴故1-a>0 恒成立,由此求得a的范围.
(2)根据|x+3|+|x-7|≥10对任意x∈R都成立,可得f(x)=lg(|x+3|+|x-7|)-a>0的解集为R,∴故1-a>0 恒成立,由此求得a的范围.
解答:
解:(1)当a=1时,原不等式可变为|x+3|+|x-7|>10,
由绝对值的意义可得|x+3|+|x-7|表示数轴上的x对应点到-3、7对应点的距离之和,
而-3和7到-3、7对应点的距离之和正好等于10,
可得其解集为{x|x<-3,或x>7}.
(2)∵|x+3|+|x-7|≥|x+3-(x-7)|=10对任意x∈R都成立.
∴f(x)=lg(|x+3|+|x-7|)-a>0的解集为R,∴1-a>0 恒成立,
∴a<1.
由绝对值的意义可得|x+3|+|x-7|表示数轴上的x对应点到-3、7对应点的距离之和,
而-3和7到-3、7对应点的距离之和正好等于10,
可得其解集为{x|x<-3,或x>7}.
(2)∵|x+3|+|x-7|≥|x+3-(x-7)|=10对任意x∈R都成立.
∴f(x)=lg(|x+3|+|x-7|)-a>0的解集为R,∴1-a>0 恒成立,
∴a<1.
点评:本题主要考查绝对值三角不等式,绝对值的意义,函数的恒成立问题,属于基础题.

练习册系列答案
相关题目
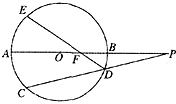 已知⊙O的半径R=2,P为直径AB延长线上一点,PB=3,割线PDC交⊙O于D,C两点,E为⊙O上一点,且
已知⊙O的半径R=2,P为直径AB延长线上一点,PB=3,割线PDC交⊙O于D,C两点,E为⊙O上一点,且