题目内容
在平面上，我们如果用一条直线去截正方形的一个角，那么截下的一个直角三角形，按图所标边长，由勾股定理有：
.设想正方形换成正方体，把截线换成如图的截面，这时从正方体上截下三条侧棱两两垂直的三棱锥
，如果用
表示三个侧面面积，
表示截面面积，那么类比得到的结论是 ．
解析试题分析：建立从平面图形到空间图形的类比，于是可猜想:，故答案为.对的证明如下：
设
，则由
两两垂直可得
在
中，由余弦定理可得
即
所以
所以
即
.
考点：合情推理中的类比推理.
练习册系列答案
导学全程练创优训练系列答案
相关题目
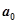，用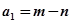
，然后继续对
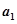重复上述变换，得数
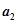，…，如此进行下去，卡普耶卡发现，无论
中，不等式
成立；在凸四边形ABCD中，
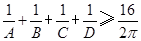成立；在凸五边形ABCDE中，不等式
成立，…，依此类推，在凸n边形
中，不等式
_____成立.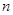
条直线，其中任何两条不平行，任何三条不共点，当
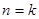时把平面分成的区域数记为
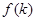,则
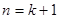时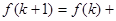
.
中可猜想出的第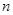
个等式是_____________
个等式为 .
(n∈N*)，则f(k＋1)－f(k)＝________.
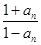(n∈N*)，则a3＝________，a1·a2·a3·…·a2007＝________．
+
+…+
<n(n∈N*,n>1)时,第一步应验证的不等式是 .