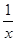题目内容
若函数f(x)= sin2ax-sinaxcosax(a>0)的图象与直线y=m(m为常数)相切,并且切点的横坐标依次成公差为(1)求m的值;
(2)若点A(x0,y0)是y=f(x)图象的对称中心,且x0∈[0,![]() ],求点A的坐标.
],求点A的坐标.
解:(1)f(x)=![]() [(1-cos2ax)-
[(1-cos2ax)-![]() sin2ax]?
sin2ax]?
=-![]() (sin2ax+cos2ax)+
(sin2ax+cos2ax)+![]() ?
?
=-![]() sin(2ax+
sin(2ax+![]() )+
)+![]() . ?
. ?
∵y=f(x)的图象与y=M相切,?
∴M为f(x)的最大值或最小值,?
即M=1+![]() 或M=1-
或M=1-![]() . ?
. ?
(2)又∵切点横坐标依次成公差为![]() 的等差数列,?
的等差数列,?
∴f(x)最小正周期为![]() .?
.?
又T=![]() =
=![]() ,a>0,∴a=2, ?
,a>0,∴a=2, ?
即f(x)=-![]() sin(4x+
sin(4x+![]() )+
)+![]() . ?
. ?
令sin(4x+![]() )=0,则4x0+
)=0,则4x0+![]() =kπ(k∈Z),?
=kπ(k∈Z),?
x0=![]() -
-![]() . ?
. ?
由0≤![]() -
-![]() ≤
≤![]() π及k∈Z.得k=1,2,3.?
π及k∈Z.得k=1,2,3.?
因此对称中心为(![]() π,
π, ![]() )、(
)、(![]() π,
π,![]() )、(
)、(![]() π,
π,![]() ).
).

 习题精选系列答案
习题精选系列答案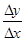 =4+2Δx
=4+2Δx