题目内容
设an表示满足不等式
的整数对(x,y)的个数(其中整数对是指x,y都为整数的有序实数对),则
(a2+a4+…a2012)=( )
|
| 1 |
| 4024 |
| A.1012 | B.2014 | C.4024 | D.4028 |
∵x>0,y>0,
∴y≤-nx2+10n即y≤n(10-x2)
①当x=1时,正整数y≤9n,共9n个整数对(x,y);②当x=2时,正整数y≤6n,共6n个整数对(x,y);
③当x=3时,正整数y≤n,共n个整数对(x,y)
由此可得,an=9n+6n+n=16n
∴a2+a4+…+a2012=16(2+4+…+2012)=16×503×(2+2012)=4024×4028
由此可得
(a2+a4+…a2012)=
×(4024×4028)=4028
故选:D
∴y≤-nx2+10n即y≤n(10-x2)
①当x=1时,正整数y≤9n,共9n个整数对(x,y);②当x=2时,正整数y≤6n,共6n个整数对(x,y);
③当x=3时,正整数y≤n,共n个整数对(x,y)
由此可得,an=9n+6n+n=16n
∴a2+a4+…+a2012=16(2+4+…+2012)=16×503×(2+2012)=4024×4028
由此可得
| 1 |
| 4024 |
| 1 |
| 4024 |
故选:D

练习册系列答案
相关题目
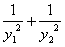 所表示的平面区域为Dn,把Dn内的整点(横、纵坐标均为整数的点)按其到原点的距离从近到远排列成点列:(x1,y1),(x2,y2),…,(xn,yn).
所表示的平面区域为Dn,把Dn内的整点(横、纵坐标均为整数的点)按其到原点的距离从近到远排列成点列:(x1,y1),(x2,y2),…,(xn,yn).