题目内容
已知函数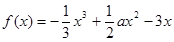 ,
,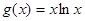
(Ⅰ)当a=4时,求函数f(x)的单调区间;
(Ⅱ)求函数g(x)在区间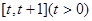 上的最小值;
上的最小值;
(Ⅲ)若存在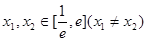 ,使方程
,使方程
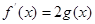 成立,求实数a的取值范围(其中e=2.71828是自然对数的底数)
成立,求实数a的取值范围(其中e=2.71828是自然对数的底数)
(Ⅰ)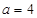 时,
时,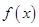 的单调增区间为
的单调增区间为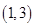 ,单调减区间为
,单调减区间为 .
.
(Ⅱ)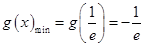 ;(III)实数
;(III)实数 的取值范围为
的取值范围为 .
.
解析试题分析:(Ⅰ)求导数,根据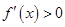 ,
,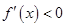 得到函数的单调区间.
得到函数的单调区间.
(Ⅱ)遵循“求导数,求驻点,讨论单调性,确定最值”.
(III) 由 可得
可得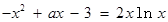
“分离参数”得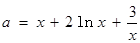 .
.
令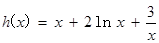 ,遵循“求导数,求驻点,讨论单调性,确定最值”.
,遵循“求导数,求驻点,讨论单调性,确定最值”.
“表解法”往往直观易懂,避免出错.
试题解析:(Ⅰ)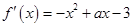 1分
1分
当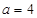 时,
时, 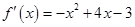 ,令
,令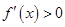 得
得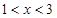 2分
2分
∴当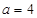 时,
时,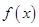 的单调增区间为
的单调增区间为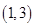 ,单调减区间为
,单调减区间为 . 3分
. 3分
(Ⅱ)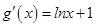 , 令
, 令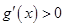 ,得
,得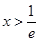 4分
4分
①当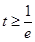 时,在区间
时,在区间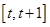 上
上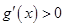 ,
, 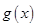 为增函数,
为增函数,
∴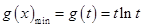 5分
5分
②当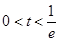 时,在区间
时,在区间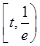 上
上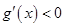 ,
,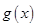 为减函数, 6分
为减函数, 6分
在区间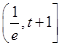 上
上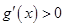 ,
,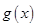 为增函数, 7分
为增函数, 7分
∴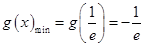 8分
8分
(III) 由 可得
可得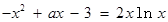
∴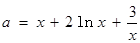 , 9分
, 9分
令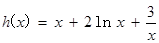 ,则
,则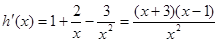 10分
10分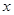
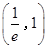
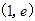
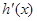
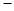

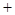
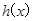
单调递减 
课课练与单元测试系列答案
世纪金榜小博士单元期末一卷通系列答案
单元测试AB卷台海出版社系列答案
黄冈新思维培优考王单元加期末卷系列答案
名校名师夺冠金卷系列答案
小学英语课时练系列答案
培优新帮手系列答案


课堂作业广西教育出版社系列答案
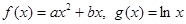 .
.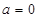 时,①若
时,①若 的图象与
的图象与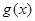 的图象相切于点
的图象相切于点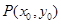 ,求
,求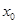 及
及 的值;
的值;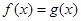 在
在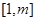 上有解,求
上有解,求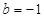 时,若
时,若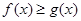 在
在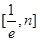 上恒成立,求
上恒成立,求 的取值范围.
的取值范围. 的正方形
的正方形 内建一个交通“环岛”.正方形的四个顶点为圆心在四个角分别建半径为
内建一个交通“环岛”.正方形的四个顶点为圆心在四个角分别建半径为 (
( 不小于
不小于 )的扇形花坛,以正方形的中心为圆心建一个半径为
)的扇形花坛,以正方形的中心为圆心建一个半径为 的圆形草地.为了保证道路畅通,岛口宽不小于
的圆形草地.为了保证道路畅通,岛口宽不小于 ,绕岛行驶的路宽均不小于
,绕岛行驶的路宽均不小于 .
.
 取
取 )
) 元
元 ,四个花坛的造价为
,四个花坛的造价为 元
元 元
元 ,
, (其中
(其中 为常数);
为常数); 和
和 有相同的极值点,求
有相同的极值点,求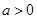 ,问是否存在
,问是否存在 ,使得
,使得 ,若存在,请求出实数
,若存在,请求出实数 ,若函数
,若函数 有5个不同的零点,求实数
有5个不同的零点,求实数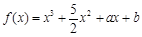 (
( 为常数),其图象是曲线
为常数),其图象是曲线 .
. 时,求函数
时,求函数 的单调减区间;
的单调减区间; ,若存在唯一的实数
,若存在唯一的实数 ,使得
,使得 与
与 同时成立,求实数
同时成立,求实数 的取值范围;
的取值范围; 为曲线
为曲线 与曲线
与曲线 ,在点
,在点 ,设切线
,设切线 的斜率分别为
的斜率分别为 .问:是否存在常数
.问:是否存在常数 ,使得
,使得 ?若存在,求出
?若存在,求出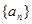 的前n项和为Sn,对一切正整数n,点
的前n项和为Sn,对一切正整数n,点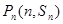 在函数
在函数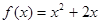 的图像上,且过点
的图像上,且过点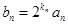 ,求数列
,求数列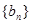 的前n项和Tn.
的前n项和Tn. ,其中
,其中 为常数.
为常数.  是区间
是区间 上的增函数,求实数
上的增函数,求实数 在
在 时恒成立,求实数
时恒成立,求实数 ,设
,设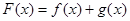
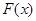 的单调区间
的单调区间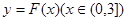 图象上任意一点
图象上任意一点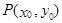 为切点的切线的斜率
为切点的切线的斜率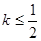 恒成立,求实数
恒成立,求实数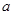 的最小值
的最小值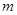 ,使得函数
,使得函数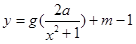 的图象与函数
的图象与函数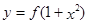 的图象恰有四个不同交点?若存在,求出实数
的图象恰有四个不同交点?若存在,求出实数 .
.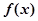 在区间
在区间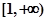 单调递增,求
单调递增,求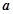 的最小值;
的最小值;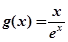 ,对
,对 ,使
,使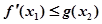 成立,求
成立,求 的范围.
的范围.