题目内容
已知函数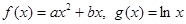 .
.
⑴当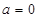 时,①若
时,①若 的图象与
的图象与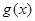 的图象相切于点
的图象相切于点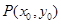 ,求
,求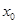 及
及 的值;
的值;
②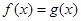 在
在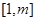 上有解,求
上有解,求 的范围;
的范围;
⑵当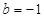 时,若
时,若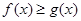 在
在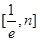 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.
(1)①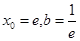 ,②
,②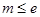 时,
时,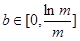 ;
;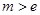 时,
时,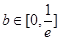 (2)
(2)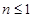 时,
时,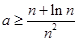 ;
; 时,
时,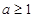 ..
..
解析试题分析:(1)①本题为曲线切线问题,一般从设切点出发,利用切点在切线上.切点在曲线上,切点处的导数值为切线的斜率三个方面建立等量关系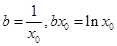 ,从而解出
,从而解出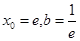 ,②方程有解问题,一般利用分离法,求函数
,②方程有解问题,一般利用分离法,求函数 值域解决.由于定义域
值域解决.由于定义域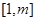 不定,需讨论极值为零的点
不定,需讨论极值为零的点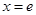 是否在定义域内,这决定了单调区间,也决定了最值.(2)不等式恒成立问题,往往转化为最值问题,这也需要分离变量. 即
是否在定义域内,这决定了单调区间,也决定了最值.(2)不等式恒成立问题,往往转化为最值问题,这也需要分离变量. 即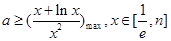 ,在求函数
,在求函数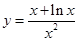 值域时,有两个难点,一是判断极值为零的点
值域时,有两个难点,一是判断极值为零的点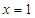 ,二是讨论极值为零的点
,二是讨论极值为零的点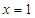 是否在
是否在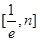 内.
内.
试题解析:⑴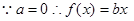
①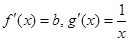
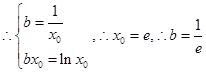 , 3分
, 3分
②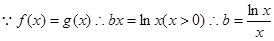 即
即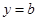 与
与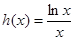 在
在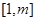 上有交点…4分
上有交点…4分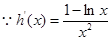 ,
,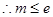 时
时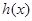 在
在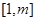 上递增,
上递增,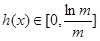 ;
;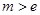 时
时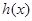 在
在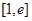 上递增,在
上递增,在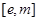 上递减且
上递减且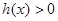 ,
,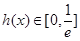 ……7分
……7分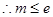 时,
时,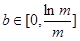 ;
;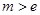 时,
时,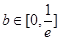 8分
8分
⑵ 即
即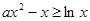 ,
,
即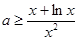 在
在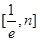 上恒成立, 9分
上恒成立, 9分
令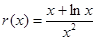 ,
,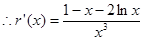
令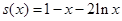 ,则
,则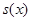 为单调减函数,且
为单调减函数,且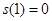 , 12分
, 12分
∴当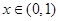 时,
时,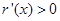 ,
,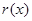 单调递增,
单调递增,
当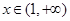 时,
时,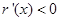 ,
,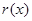 单调递减, 13分
单调递减, 13分
若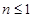 ,则
,则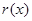 在
在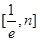 上单调递增,
上单调递增,
∴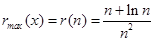 ,∴
,∴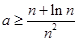 ;
;
若 ,则
,则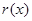 在
在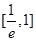 上单调递增,
上单调递增,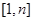 单调递减,
单调递减,
∴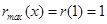 ,∴
,∴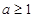 15分
15分
∴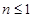 时,
时,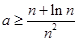 ;
; 时,
时,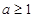 . 16分
. 16分
考点:利用导数求切线,利用导数求最值.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
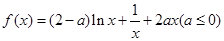 .
.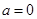 时,求
时,求 的极值;
的极值;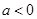 时,讨论
时,讨论 ,
,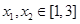 ,恒有
,恒有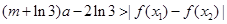 成立,求实数
成立,求实数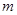 的取值范围.
的取值范围. ,
,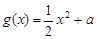 (
( 为常数),直线
为常数),直线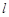 与函数
与函数 、
、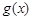 的图象都相切,且
的图象都相切,且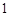 .
.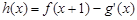 [注:
[注: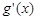 是
是 的单调递增区间;
的单调递增区间;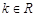 时,试讨论方程
时,试讨论方程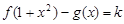 的解的个数.
的解的个数.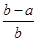 <ln
<ln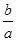 <
<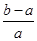 ,其中0<a<b;
,其中0<a<b; + +
+ + ]≤1+[lnn](n∈N*).
]≤1+[lnn](n∈N*).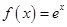 .
.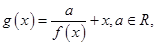 求
求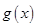 的极值.
的极值.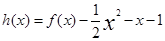 在
在 上为增函数。
上为增函数。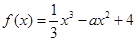 ,且
,且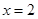 是函数
是函数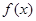 的一个极小值点.
的一个极小值点.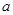 的值;
的值;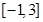 上的最大值和最小值.
上的最大值和最小值.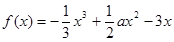 ,
,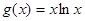
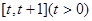 上的最小值;
上的最小值;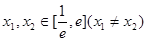 ,使方程
,使方程
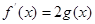 成立,求实数a的取值范围(其中e=2.71828是自然对数的底数)
成立,求实数a的取值范围(其中e=2.71828是自然对数的底数)