Question

空间四边形ABCD中，已知AD=1，BC=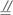，且AD⊥BC，对角线BD=，AC=，求异面直线AC与BD所成的角.

Answer 1

解析:取AB、BC、CD、BD的中点分别为E、F、G、H.连结EF、EH、EG、FG、HG,则EHAD，FGBD，HGBC,EFAC.

∴EH=，FG=，HG=，EF=，

EF与FG所成的角就是AC与BD所成的角.

∵AD⊥BC,∴EH⊥HG.

在Rt△EHG中，

EG²=EH²+HG²=.

在△EFG中，EF²+FG²=.

而EG²=1，∴∠EFG=90°.

∴异面直线AC与BD所成的角为90°.