题目内容
如图1-2-7所示，DE∥BC，EF∥DC，求证:AD2=AF·AB.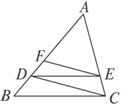
图1-2-7
思路分析：要证AD2=AF·AB，只要证
，由于AF、AD、AB在同一直线上，因此上式不能直接用定理证，于是想到用过渡比.从基本图形“A”型中立即可找到过渡比为
.
证明：∵DE∥BC，
∴
(平行于三角形一边的直线截其他两边所得的对应线段成比例).
∵EF∥DC,∴
.
∴
,即AD2=AF·AB.
深化升华 等积式常常转化为比例式证明，要善于从复杂图形中识别出基本图形中的公共部分(即
)，它往往是构成证明中的过渡比.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
