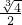Question

方程x³-bx²+1=0有且仅有两个不同零点，则b的值为（　　）

• A．

  3 4

  2

• B．

  3 2

  2

• C．

  3

  2

  3	2

• D．不确定

Answer 1

分析：题意可得，函数f（x）=x³-bx² 和直线y=-1 只有两个交点，利用导数求得函数的极值f（0）=0，f（

2b

3

）=-

4

27

b³．令-

4

27

b³=-1，解得 b的值．

解答：解：∵方程x³-bx²+1=0有且仅有两个不同零点，故函数f（x）=x³-bx² 和直线y=-1 只有两个交点．
令f′（x）=3x²-2bx=0，可得 x=0，或 x=

2b

3

．
故当 x=0，或 x=

2b

3

时，函数f（x）取得极值．
而f（0）=0，f（

2b

3

）=

8

27

b³-

4

9

b³=-

4

27

b³．
令-

4

27

 b³=-1，解得 b=

3

2

3	2

，
故选C．

点评：本题主要考查函数的零点的定义，函数的零点与方程的根的关系，体现了转化的数学思想，属于中档题．