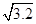题目内容
先在甲、乙两个靶.某射手向甲靶射击一次,命中的概率为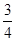 ,命中得
,命中得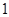 分,没有命中得
分,没有命中得 分;向乙靶射击两次,每次命中的概率为
分;向乙靶射击两次,每次命中的概率为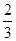 ,每命中一次得
,每命中一次得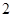 分,没有命中得
分,没有命中得 分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
(Ⅰ)求该射手恰好命中一次的概率;
(Ⅱ)求该射手的总得分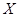 的分布列及数学期望
的分布列及数学期望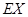 .
.
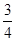 ,命中得
,命中得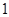 分,没有命中得
分,没有命中得 分;向乙靶射击两次,每次命中的概率为
分;向乙靶射击两次,每次命中的概率为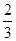 ,每命中一次得
,每命中一次得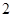 分,没有命中得
分,没有命中得 分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.(Ⅰ)求该射手恰好命中一次的概率;
(Ⅱ)求该射手的总得分
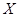 的分布列及数学期望
的分布列及数学期望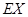 .
.: (Ⅰ) (Ⅱ)
(Ⅱ)
 (Ⅱ)
(Ⅱ)
: (Ⅰ)记“该射手恰好命中一次”为事件 ,“该射手射击甲靶命中”为事件
,“该射手射击甲靶命中”为事件 ,“该射手第一次射击乙靶命中”为事件
,“该射手第一次射击乙靶命中”为事件 ,“该射手第二次射击乙靶命中”为事件
,“该射手第二次射击乙靶命中”为事件 .
.
由题意知 ,
, .
.
由于 ,
,
所以

(Ⅱ)根据题意,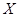 的所有可能取值为
的所有可能取值为
 ,
,





所以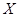 的分布列为
的分布列为

【考点定位】本题考查了独立事件、互斥事件的识别及应用,并对离散型随机变量的分布列与数学期望进一步考查,难度较小,但要注意对不同事件的描述,便于书写步骤
 ,“该射手射击甲靶命中”为事件
,“该射手射击甲靶命中”为事件 ,“该射手第一次射击乙靶命中”为事件
,“该射手第一次射击乙靶命中”为事件 ,“该射手第二次射击乙靶命中”为事件
,“该射手第二次射击乙靶命中”为事件 .
.由题意知
 ,
, .
.由于
 ,
,所以

(Ⅱ)根据题意,
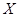 的所有可能取值为
的所有可能取值为
 ,
,




所以
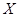 的分布列为
的分布列为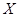 |  | 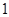 | 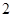 |  |  |  |
 |  |  |  |  |  |  |

【考点定位】本题考查了独立事件、互斥事件的识别及应用,并对离散型随机变量的分布列与数学期望进一步考查,难度较小,但要注意对不同事件的描述,便于书写步骤

练习册系列答案
相关题目
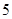 枚均匀的硬币
枚均匀的硬币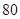 次,设
次,设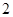 枚正面向上,
枚正面向上,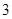 枚反面向上的次数为
枚反面向上的次数为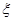 ,则
,则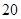

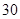
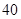
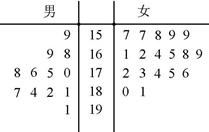
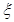 表示所选代表中女“运动健将”的人数,试写出
表示所选代表中女“运动健将”的人数,试写出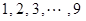 班参加高考体检,
班参加高考体检,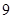 个班中,任选
个班中,任选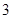 个班先参加视力检查. (I)求这
个班先参加视力检查. (I)求这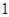 个班班级序号是偶数的概率;
个班班级序号是偶数的概率;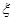 为这
为这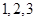 班,则有两组相邻的,
班,则有两组相邻的,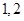 班和
班和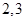 班,此时
班,此时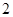 ).求随机变量
).求随机变量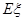 .
.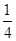 ,不堵车的概率为
,不堵车的概率为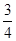 ;汽车走公路②堵车的概率为
;汽车走公路②堵车的概率为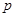 ,不堵车的概率为
,不堵车的概率为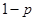 ,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。(I)若三辆车中恰有一辆车被堵的概率为
,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。(I)若三辆车中恰有一辆车被堵的概率为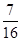 ,求走公路②堵车的概率;(Ⅱ)在(I)的条件下,求三辆车中被堵车辆的个数
,求走公路②堵车的概率;(Ⅱ)在(I)的条件下,求三辆车中被堵车辆的个数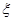 的分布列和数学期望。
的分布列和数学期望。 五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.
五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.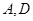 区域同时用红色鲜花时,求布置花圃的不同方法的种数;
区域同时用红色鲜花时,求布置花圃的不同方法的种数; 为花圃中用红色鲜花布置的区域的个数,求随机变量
为花圃中用红色鲜花布置的区域的个数,求随机变量
 元奖金.假设顾客每次抽奖时获奖与否的概率都是
元奖金.假设顾客每次抽奖时获奖与否的概率都是 ,
, 元的概率;
元的概率; .请写出
.请写出 分.
分.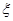 的分布列为下表所示:
的分布列为下表所示:
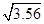 C.3.2 D.
C.3.2 D.