题目内容
在ABCD中，已知AB=CD=a,AD=BC=2a,∠A=60°,AC∩BD=E，将其沿对角线BD折成直二面角(如图).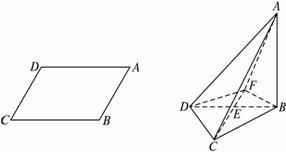
(1)证明AB⊥平面BCD；
(2)证明平面ACD⊥平面ABD；
(3)求二面角ACEB的大小.
解析：(1)证明：在△ABD中，由AB=a,AD=2a,∠A=60°,可得∠ABD=90°.?
又二面角A-BD-C为直二面角,AB
面ABD，面ABD∩面BCD=DB,∴AB⊥平面BCD.?
(2)证明：由(1)知AB⊥平面BCD，CD
平面BCD，?
∴AB⊥CD.?
同样，仿(1)可证明CD⊥BD.?
而AB∩BD=B，∴CD⊥平面ABD.?
而CD
平面ACD，∴平面ACD⊥平面ABD.?
(3)由(1)可得AB⊥平面BCD，过点B作BF⊥CE于F,连结AF，则由三垂线定理可得AF⊥CE.?
∴∠AFB即为二面角A-CE-B的平面角.?
由条件可得BF=
.?
在△BFA中，tan∠BAF=
.?
故二面角A-CE-B的大小为arctan
.
练习册系列答案
阅读快车系列答案
相关题目
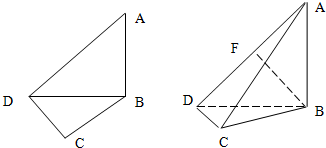如图，在平面四边形ABCD中，已知∠A=45°，∠C=90°，∠ADC=105°，AB=BD，现将四边形ABCD沿BD折起，使平面ABD⊥平面BDC，设点F为棱AD的中点．
，－7)，B(2，6)，其对角线的交点M(3，
)，则C、D的坐标分别是________．
ABCD中，已知
=a，
=b. 
、
；
ABCD为矩形.