题目内容
(文)已知椭圆 =1内一点A(1,1),则过点A且被该点平分的弦所在直线的方程是________.
=1内一点A(1,1),则过点A且被该点平分的弦所在直线的方程是________.
x+4y-5=0
分析:设过A点的直线与椭圆两交点的坐标,分别代入椭圆方程,得到两个关系式,分别记作①和②,①-②后化简得到一个关系式,然后根据A为弦EF的中点,由A的坐标求出E和F两点的横纵坐标之和,表示出直线EF方程的斜率,把化简得到的关系式变形,将E和F两点的横纵坐标之和代入即可求出斜率的值,然后由点A的坐标和求出的斜率写出直线EF的方程即可.
解答:设过点A的直线与椭圆相交于两点,E(x1,y1),F(x2,y2),
则有 =1①,
=1①, =1②,
=1②,
①-②式可得: =0,
=0,
又点A为弦EF的中点,且A(1,1),∴x1+x2=2,y1+y2=2,
即得kEF= ,
,
∴过点A且被该点平分的弦所在直线的方程是y-1= ,即x+4y-5=0.
,即x+4y-5=0.
故答案为:x+4y-5=0
点评:本题考查了直线与椭圆的位置关系及中点弦问题的求解策略,关键在于对“设而不求法”的掌握.
分析:设过A点的直线与椭圆两交点的坐标,分别代入椭圆方程,得到两个关系式,分别记作①和②,①-②后化简得到一个关系式,然后根据A为弦EF的中点,由A的坐标求出E和F两点的横纵坐标之和,表示出直线EF方程的斜率,把化简得到的关系式变形,将E和F两点的横纵坐标之和代入即可求出斜率的值,然后由点A的坐标和求出的斜率写出直线EF的方程即可.
解答:设过点A的直线与椭圆相交于两点,E(x1,y1),F(x2,y2),
则有
 =1①,
=1①, =1②,
=1②,①-②式可得:
 =0,
=0,又点A为弦EF的中点,且A(1,1),∴x1+x2=2,y1+y2=2,
即得kEF=
 ,
,∴过点A且被该点平分的弦所在直线的方程是y-1=
 ,即x+4y-5=0.
,即x+4y-5=0.故答案为:x+4y-5=0
点评:本题考查了直线与椭圆的位置关系及中点弦问题的求解策略,关键在于对“设而不求法”的掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

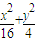 =1内一点A(1,1),则过点A且被该点平分的弦所在直线的方程是 .
=1内一点A(1,1),则过点A且被该点平分的弦所在直线的方程是 .