题目内容
设全集U=R，集合P={x|-2≤x≤2}，M={x|x2-2x-3≤0}，则（∁UP）∩M等于（ ）
| A、{x|-2≤x≤2} |
| B、{x|2＜x≤3} |
| C、{x|2≤x≤3} |
| D、{x|-1＜x≤3} |
考点：交、并、补集的混合运算
专题：集合
分析：求出M中不等式的解集确定出M，根据全集U=R及P求出P的补集，找出P补集与M的交集即可．
解答：
解：由M中不等式变形得：（x-3）（x+1）≤0，
解得：-1≤x≤3，即M={x|-1≤x≤3}，
∵全集U=R，集合P={x|-2≤x≤2}，
∴∁UP={x|x＜-2或x＞2}，
则（∁UP）∩M={x|2＜x≤3}，
故选：B．
解得：-1≤x≤3，即M={x|-1≤x≤3}，
∵全集U=R，集合P={x|-2≤x≤2}，
∴∁UP={x|x＜-2或x＞2}，
则（∁UP）∩M={x|2＜x≤3}，
故选：B．
点评：此题考查了交、并、补集的混合运算，熟练掌握各自的定义是解本题的关键．
练习册系列答案
教材全解字词句篇系列答案
相关题目
已知{an}是等比数列，其前n项和为Sn，若
=9，则
=（ ）
| S6 |
| S3 |
| S12 |
| S6 |
| A、9 | B、18 | C、64 | D、65 |
已知集合A={y|y=x2+2，x∈R}，B={y|y=4-x，x∈R}，则A∩B=（ ）
| A、{3，6} | B、{-2，1} |
| C、{y|y≥2} | D、R |
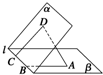如图所示，已知二面角α-l-β的平面角为θ（θ∈（0，