题目内容
15.已知3sin2θ=5cosθ+1,则cos(π+2θ)=$\frac{7}{9}$.分析 根据同角三角函数关系式化简3sin2θ=5cosθ+1,利用二倍角公式化简cos(π+2θ)可得答案.
解答 解:由3sin2θ=5cosθ+1,
可得:3(1-cos2θ)=5cosθ+1
3cos2θ+5cosθ-2=0,即(3cosθ-1)(cosθ+2)=0,
∴cosθ=$\frac{1}{3}$.
那么:cos(π+2θ)=-cos2θ=-(2cos2θ-1)=1-2cos2θ=1-2×$\frac{1}{9}$=$\frac{7}{9}$.
故答案为$\frac{7}{9}$.
点评 本题主要考查了同角三角函数关系式和二倍角公式的应用,属于基本知识的考查.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
5.设函数f(x)=|x2-2x-1|,若m>n>1,且f(m)=f(n),则(m-1)(n-1)的取值范围为( )
| A. | (0,2) | B. | (0,2] | C. | (1,2) | D. | (1,2] |
3.若$\overline z$是z的共轭复数,且满足$\overline z({1-i})$=3+i,则z=( )
| A. | 1+2i | B. | -1+2i | C. | 1-2i | D. | -1-2i |
7.执行如图所示的程序框图,如图输出S的值为-1,那么判断框内应填入的条件是( )
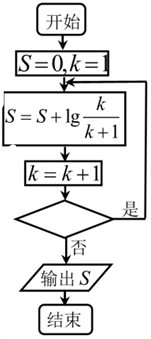

| A. | k≤8 | B. | k≤9 | C. | k≤10 | D. | k≤11 |
 一儿童游乐场拟建造一个“蛋筒”型游乐设施,其轴截面如图中实线所示.ABCD是等腰梯形,AB=20米,∠CBF=α(F在AB的延长线上,α为锐角).圆E与AD,BC都相切,且其半径长为100-80sinα米.EO是垂直于AB的一个立柱,则当sinα的值设计为多少时,立柱EO最矮?
一儿童游乐场拟建造一个“蛋筒”型游乐设施,其轴截面如图中实线所示.ABCD是等腰梯形,AB=20米,∠CBF=α(F在AB的延长线上,α为锐角).圆E与AD,BC都相切,且其半径长为100-80sinα米.EO是垂直于AB的一个立柱,则当sinα的值设计为多少时,立柱EO最矮?