题目内容

抛物线x²=-2py（p＞0）的焦点到其准线的距离是

A.
$数学公式$
B.
p
C.
2p
D.
4p

B
分析：利用抛物线的标准方程可得，焦点到准线的距离为p，从而得到结果．
解答：根据抛物线的性质，
∵抛物线x²=-2py（p＞0）
∴焦点坐标为（0，- $\text{[math]}$ ），准线方程为：x= $\text{[math]}$ ，
则抛物线x²=-2py（p＞0）的焦点到准线的距离为p，
故选B．
点评：本题考查抛物线的标准方程，以及简单性质的应用，判断焦点到准线的距离为p是解题的关键．

练习册系列答案

导学与训练系列答案

导与学学案导学系列答案

地道中考系列答案

地理图册系列答案

第一测评系列答案

点金系列答案

点睛学案系列答案

夺冠金卷单元同步测试系列答案

夺冠课时导学案系列答案

发现会考系列答案

相关题目

设直线l过抛物线x²=2py（p＞0）的焦点F，且与该抛物线交于A、B两点，l的斜率为k，点C（0，t），当k=0，t=1+2

时，△ABC为等边三角形．
（Ⅰ）求抛物线的方程．
（Ⅱ）若不论实数k取何值，∠ACB始终为钝角，求实数t的取值范围．

如图，已知⊙C过焦点A（0，P）（P＞0）圆心C在抛物线x²=2py上运动，若MN为⊙C在x轴上截得的弦，设|AM|=l₁，|AN|=l₂，∠MAN=θ
（1）当C运动时，|MN|是否变化？证明你的结论．
（2）求

的最大值，并求出取最大值时θ值及此时⊙C方程．

（2013•枣庄二模）已知抛物线x²=2py上点（2，2）处的切线经过椭圆E：

=1(a＞b＞0)的两个顶点．
（1）求椭圆E的方程；
（2）过椭圆E的上顶点A的两条斜率之积为-4的直线与该椭圆交于B、C两点．请问：是否存在一点D，使得直线BC恒过该点？若存在，请求出定点D的坐标；若不存在，请说明理由；
（3）在（2）的条件下，过点A作直线BC的垂线，垂足为H，求点H的轨迹方程．

点M（m，4）m＞0为抛物线x²=2py（p＞0）上一点，F为其焦点，已知|FM|=5，
（1）求m与p的值；
（2）以M点为切点作抛物线的切线，交y轴与点N，求△FMN的面积．

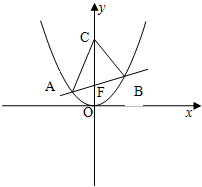
设抛物线x²=2py（p＞0）的焦点为F，经过点F的直线交抛物线于A、B两点，分别过A、B两点作抛物线的两条切线交于点C，则有（　　）