题目内容
设抛物线x2=2py(p>0)的焦点为F,经过点F的直线交抛物线于A、B两点,分别过A、B两点作抛物线的两条切线交于点C,则有( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:设出过点F的直线方程,和抛物线方程联立后由根与系数关系得到两交点的横纵坐标的和与积,把抛物线所对应的函数求导后得到A,B两点处的切线的斜率,由点斜式得到过A,B两点的切线方程,由两切线方程联立求得C点的坐标,代入
•
可得结论.
| AC |
| BC |
解答:解:∵F(0,
),又依题意直线l不与x轴垂直,∴设直线l的方程为y=kx+
.
由
,可得x2-2pkx-p2=0.
设A(x1,y1),B(x2,y2),则x1+x2=2pk,x1x2=-p2.
y1+y2=k(x1+x2)+p=2pk2+p,
y1y2=(kx1+
)(kx2+
)=k2x1x2+
(x1+x2)+
=-k2p2+k2p2+
=
.
由x2=2py,可得y=
,∴y′=
.
∴抛物线在A,B两点处的切线的斜率分别为
,
.
∴在点A处的切线方程为y-y1=
(x-x1),
即y=
x-
.
同理在点B处的切线方程为y=
x-
.
解方程组
,可得
.
∴点C的坐标为(pk,-
).
∴
•
=(pk-x1,-
-y1)•(pk-x2,-
-y2)
=p2k2-pk(x1+x2)+x1x2+
+
(y1+y2)+y1y2
=p2k2-pk•2pk-p2+
+
•(2pk2+p)+
=0.
故选:A.
| p |
| 2 |
| p |
| 2 |
由
|
设A(x1,y1),B(x2,y2),则x1+x2=2pk,x1x2=-p2.
y1+y2=k(x1+x2)+p=2pk2+p,
y1y2=(kx1+
| p |
| 2 |
| p |
| 2 |
| kp |
| 2 |
| p2 |
| 4 |
=-k2p2+k2p2+
| p2 |
| 4 |
| p2 |
| 4 |
由x2=2py,可得y=
| x2 |
| 2p |
| x |
| p |
∴抛物线在A,B两点处的切线的斜率分别为
| x1 |
| p |
| x2 |
| p |
∴在点A处的切线方程为y-y1=
| x1 |
| p |
即y=
| x1 |
| p |
| x12 |
| 2p |
同理在点B处的切线方程为y=
| x2 |
| p |
| x22 |
| 2p |
解方程组
|
|
∴点C的坐标为(pk,-
| p |
| 2 |
∴
| AC |
| BC |
| p |
| 2 |
| p |
| 2 |
=p2k2-pk(x1+x2)+x1x2+
| p2 |
| 4 |
| p |
| 2 |
=p2k2-pk•2pk-p2+
| p2 |
| 4 |
| p |
| 2 |
| p2 |
| 4 |
故选:A.
点评:本题考查了直线与圆锥曲线的关系,考查了平面向量的数量积运算,涉及直线与圆锥曲线的关系问题,常采用联立方程组,化为关于x的方程后利用一元二次方程根与系数的关系解决,是有一定难度题目.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 已知圆C的圆心在抛物线x2=2py(p>0)上运动,且圆C过A(0,p)点,若MN为圆C在x轴上截得的弦.
已知圆C的圆心在抛物线x2=2py(p>0)上运动,且圆C过A(0,p)点,若MN为圆C在x轴上截得的弦. (2013•杭州二模)如图,已知直线y=2x-2与抛物线x2=2py(p>0)交于M1,M2两点,直线y=
(2013•杭州二模)如图,已知直线y=2x-2与抛物线x2=2py(p>0)交于M1,M2两点,直线y=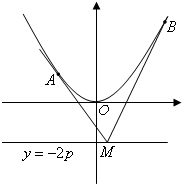 如图,设抛物线x2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B.求证:A,M,B三点的横坐标成等差数列.
如图,设抛物线x2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B.求证:A,M,B三点的横坐标成等差数列. =
=  ;
; +
+ =1(a>b>0)提出一个有深度的结论,并证明之.
=1(a>b>0)提出一个有深度的结论,并证明之.