题目内容
7.设等差数列{an}的前n项和为Sn,已知a3=24,S11=0(Ⅰ)求数列{an}的前n项和Sn;
(Ⅱ)设bn=$\frac{{S}_{n}}{n}$,求数列{bn}前n项和Tn的最大值.
分析 (Ⅰ)分别利用等差数列的通项公式及等差数列的前n项和的公式由a3=24,S11=0表示出关于首项和公差的两个关系式,联立即可求出首项与公差,利用等差数列的前n项和的公式即可表示出Sn;
(Ⅱ)求出数列{bn}前n项和公式得到Tn是关于n的开口向下的二次函数,根据n为正整数,利用二次函数求最值的方法求出Tn的最大值即可.
解答 解:(Ⅰ)依题意有$\left\{\begin{array}{l}{{a}_{1}+2d=24}\\{11{a}_{1}+\frac{11×10}{2}d=0}\end{array}\right.$,
解之得$\left\{\begin{array}{l}{{a}_{1}=40}\\{d=-8}\end{array}\right.$,∴Sn=$\frac{(40+48-8n)n}{2}$=-4n2+44n.
(Ⅱ)∵Sn=-4n2+44n
∴bn=$\frac{{S}_{n}}{n}$=44-4n,
∴bn+1-bn=-4
∴{bn}为等差数列,
∴Tn=$\frac{1}{2}$(40+44-4n)n=(42-2n)n=-2n2+42n=-2(n-$\frac{21}{2}$)2+$\frac{441}{2}$
故当n=10或n=11时,Tn最大,且Tn的最大值为220.
点评 此题考查学生灵活运用等差数列的通项公式及前n项和的公式,灵活运用二次函数求最值的方法解决实际问题,是一道中档题.

练习册系列答案
相关题目
18.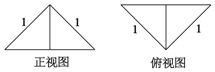 把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为( )
把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为( )
 把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为( )
把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{1}{4}$ |
17.已知集合A={x|x2-2x>0},$B=\{x|\frac{x-2}{2x}≤1\}$,则A∩B=( )
| A. | [-2,0) | B. | (-2,0)∪(2,+∞) | C. | (-∞,-2]∪(2,+∞) | D. | [-1,0]∪[2,+∞) |
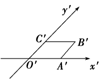 在直观图(如图所示)中,四边形O'A'B'C'为菱形且边长为2cm,则在xOy坐标系中,四边形OABC的面积为8cm2.
在直观图(如图所示)中,四边形O'A'B'C'为菱形且边长为2cm,则在xOy坐标系中,四边形OABC的面积为8cm2.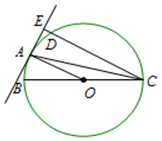 如图所示,BC 为⊙O 的直径,$\widehat{AB}=\widehat{AD}$,以点 A 为切点的切线与 CD 的延长线交于点E
如图所示,BC 为⊙O 的直径,$\widehat{AB}=\widehat{AD}$,以点 A 为切点的切线与 CD 的延长线交于点E