题目内容
20.设函数![]() 为奇函数,其图象在点
为奇函数,其图象在点![]() 处的切线与直线
处的切线与直线![]() 垂直,导函数
垂直,导函数![]() 的最小值为
的最小值为![]()
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求函数![]() 的单调递增区间,并求函数
的单调递增区间,并求函数![]() 在
在![]() 上的最大值和最小值.
上的最大值和最小值.
本题考察函数的奇偶性、单调性、二次函数的最值、导数的运用等基础知识,以及推理能力和运算能力。
解:(Ⅰ)∵![]() 为奇函数 ∴
为奇函数 ∴![]()
即![]()
![]()
∵![]() 的最小值为
的最小值为![]() ∴
∴![]()
又直线![]() 的斜率为
的斜率为![]()
因此![]()
故![]()
(Ⅱ)![]()
![]() ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
| ↗ | 极大 | ↘ | 极小 | ↗ |
所以函数![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]()
∵![]()
∴当![]() 时,
时,![]() 取得最小值为
取得最小值为![]()
当![]() 时,
时,![]() 取得最大值为
取得最大值为![]()

练习册系列答案
相关题目

 为奇函数,其图象在点
为奇函数,其图象在点 处的切线与直线
处的切线与直线 垂直,导函数
垂直,导函数 的最小值为
的最小值为 .试求
.试求 ,
, ,
, 的值。
的值。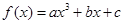
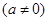 为奇函数,其图象在点
为奇函数,其图象在点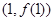 处的切线与直线
处的切线与直线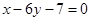 垂直,导函数
垂直,导函数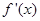 的最小值为
的最小值为 .
.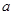 ,
,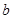 ,
,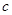 的值;
的值;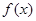 的单调递增区间,并求函数
的单调递增区间,并求函数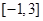 上的最大值和最小值.
上的最大值和最小值.