题目内容
设函数![]()
![]() 为奇函数,其图象在点
为奇函数,其图象在点![]() 处的切线与直线
处的切线与直线![]() 平行,导函数
平行,导函数![]() 的最小值为
的最小值为![]()
![]()
(Ⅰ)求![]() ,
,![]() ,
,![]() 的值;
的值;
(Ⅱ)求函数![]() 的单调递增区间,并求函数
的单调递增区间,并求函数![]() 在
在![]() 上的最大值和最小值
上的最大值和最小值 ![]()
(Ⅰ)![]() ,
,![]() ,
,![]()
(Ⅱ)![]() 在
在![]() 上的最大值是
上的最大值是![]() ,最小值是
,最小值是![]()
解析:
(Ⅰ)∵![]() 为奇函数,∴
为奇函数,∴![]()
即![]() ∴
∴![]() …………………2分
…………………2分
∵![]() 的最小值为
的最小值为![]() ∴
∴![]()
又直线![]() 的斜率为
的斜率为![]() 因此,
因此,![]()
∴![]() ,
,![]() ,
,![]() ………………………………………5分
………………………………………5分
(Ⅱ)由(Ⅰ)知![]()
∴![]() ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极大 |
| 极小 |
|
所以函数![]() 的单调增区间是
的单调增区间是![]() 和
和![]() …………8分
…………8分
∵![]() ,
,![]() ,
,![]()
∴![]() 在
在![]() 上的最大值是
上的最大值是![]() ,最小值是
,最小值是![]()

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目

 为奇函数,其图象在点
为奇函数,其图象在点 处的切线与直线
处的切线与直线 垂直,导函数
垂直,导函数 的最小值为
的最小值为 .试求
.试求 ,
, ,
, 的值。
的值。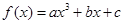
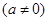 为奇函数,其图象在点
为奇函数,其图象在点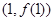 处的切线与直线
处的切线与直线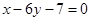 垂直,导函数
垂直,导函数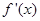 的最小值为
的最小值为 .
.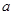 ,
,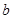 ,
,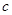 的值;
的值;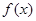 的单调递增区间,并求函数
的单调递增区间,并求函数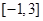 上的最大值和最小值.
上的最大值和最小值.