Question

已知正三棱锥的侧棱长为2，底面周长为9，求这个棱锥的高及体积．

Answer 1

分析：由正三棱锥的底面周长可知底面△的边长，可求出底面△ABC的面积，顶点S在底面ABC上的射影为△ABC的中心O，又在Rt△SOC中，由勾股定理求得高SO，这样可以求得三棱锥的体积．

解答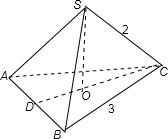：解：如图：∵S-ABC为正三棱锥        
∴S在平面ABC上的射影为△ABC的中心O．
又SC=2，△ABC的周长是L_△ABC=9，∴AB=3
∴CD=

3

2

•AB=

3 3

2

，CO=

2

3

•CD=

3

，
∴三棱锥的高SO=

SC2-CO2

=1；
所以，三棱锥的体积V_S-ABC=

1

3

S_△ABC×SO=

1

3

•

1

2

•3•3•sin60^°•1=

3 3

4

．

点评：本题考查了求三棱锥的体积，其关键是求底面积和高，求底面积时用到正弦定理的推论，求高时用到勾股定理，有综合性．