题目内容
已知抛物线y2=nx(n<0)与双曲线
-
=1有一个相同的焦点,则动点(m,n)的轨迹是( )
| x2 |
| 8 |
| y2 |
| m |
分析:根据抛物线的方程求出抛物线焦点坐标F(
,0)也是双曲线的焦点,根据双曲线的方程中三个参数的关系得到8+m=
即为n2=16m+64(n<0)得到动点(m,n)的轨迹是抛物线的一部分.
| n |
| 4 |
| n2 |
| 16 |
解答:解:抛物线焦点坐标F(
,0)根据题意,也是双曲线的焦点
则有8+m=
n2=16m+64(n<0)
所以动点(m,n)的轨迹是抛物线的一部分.
故选C.
| n |
| 4 |
则有8+m=
| n2 |
| 16 |
n2=16m+64(n<0)
所以动点(m,n)的轨迹是抛物线的一部分.
故选C.
点评:本题考查双曲线中三个参数的关系为:c2=a2+b2注意与椭圆中三个参数关系的区别:a2=c2+b2,属于基础题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
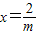 y2=nx(n<0)(m<0)与椭圆
y2=nx(n<0)(m<0)与椭圆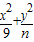 =1有一个相同的焦点,则动点(m,n)的轨迹是( )
=1有一个相同的焦点,则动点(m,n)的轨迹是( )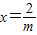 y2=nx(n<0)(m<0)与椭圆
y2=nx(n<0)(m<0)与椭圆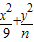 =1有一个相同的焦点,则动点(m,n)的轨迹是( )
=1有一个相同的焦点,则动点(m,n)的轨迹是( )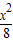 -
-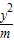 =1有一个相同的焦点,则动点(m,n)的轨迹是( )
=1有一个相同的焦点,则动点(m,n)的轨迹是( )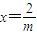 y2=nx(n<0)(m<0)与椭圆
y2=nx(n<0)(m<0)与椭圆 =1有一个相同的焦点,则动点(m,n)的轨迹是( )
=1有一个相同的焦点,则动点(m,n)的轨迹是( )